
2007-2008学年度东营市利津县八校联考
初三数学试题
一、选择题(4分×10=40分)
1、使等式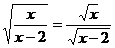 成立的
成立的 的取值范围是
的取值范围是
A.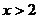 B.
B.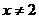 C.
C.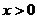 D.
D.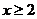
2、已知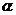 、
、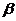 是关于
是关于 的一元二次方程
的一元二次方程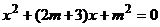 的两个不相等的实数根,且满足
的两个不相等的实数根,且满足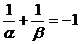 ,则
,则 的值是
的值是
A.3或-1 B.
3、化简二次根是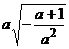 的正确结果
的正确结果
A.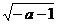 B.
B.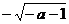 C.
C.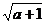 D.
D.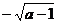
4、已知方程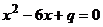 可以配方成的
可以配方成的 形式,那么
形式,那么 可以配方成下列的
可以配方成下列的
A.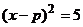 B.
B.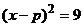
C.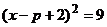 D.
D.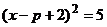
5、方程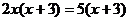 的根为
的根为
A. B.
B.
C. D.
D.
6、当 时,化简
时,化简 的结果为
的结果为
A.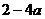 B.2 C.
B.2 C. D.0
D.0
7、关于 的一元二次方程
的一元二次方程 有两个实数根,那么
有两个实数根,那么 的取值范围是
的取值范围是
A. B.
B. 或
或
C. 或
或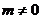 D.
D.
8、对于一元二次方程 说法正确的是
说法正确的是
A.方程的两根之和为4 B.方程的两根之积为5
C.方程有两个不等实根 D.方程没有实数根
9、下列图形既是轴对称图形又是中心对称图形的是

10、如果表示实数 、
、 的点在数轴上的位置如下图所示,那么化简
的点在数轴上的位置如下图所示,那么化简 的结果是
的结果是

A. B.
B. C.
C. D.
D.
二、填空题(4分×5=20分)
11、若 ,则
,则 的取值范围是
。
的取值范围是
。
12、若方程 有两个不相等的实数根,则
有两个不相等的实数根,则 的取值
。
的取值
。
13、如下图是两张全等的图案,它们完全地叠放在一起,按住下面的图案不动,将上面的图案绕点O顺时针旋转至少 度角度后,两种图案构成的图形是中心对称图形。

14、点P的坐标( ,
, ),满足
),满足 ,则P点关于原点对称的点Q的坐标为
。
,则P点关于原点对称的点Q的坐标为
。
15、已知实数 、
、 满足等式
满足等式 ,
, ,则
,则 。
。
三、解答题(共60分)
16、(1)(5分)计算
(2)(5分)计算
17、解方程(5分×4=20分)
(1) (2)
(2)
(3) (4)
(4)
18、先化简,再求值。(10分)
已知 ,
, ,求
,求 的值。
的值。
19、新华商场销售某种冰箱,每台进货价格为2500元,市场调研表明:当销售价位2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?(10分)
20、(10分)
已知关于 的方程
的方程 。
。
(1)求证:这个方程总有两个实数根。
(2)若等腰三角形ABC的一边长 ,另两边长
,另两边长 、
、 恰好是这个方程的两个实数根,求△ABC的周长。
恰好是这个方程的两个实数根,求△ABC的周长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com