
2007年北京市海淀区第二学期期末练习
九年级数学试题
一、选择题(本题共32分,每小题4分。)
在下列各题的四个备选答案中,只有一个是正确的。
1. 6的绝对值是
6的绝对值是
A.6 B.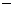
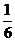 D.
D.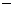
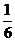
2.大脑的表面由一层薄膜所覆盖,如果把这一层薄膜铺开,约有一张报纸版面那么大,它由约l50亿个神经细胞构成,是信息接收和发送的庞大机构。150亿用科学记数法表示为
A.150×108 B.15×109 C.1.5×1010 D.0.15×1011
3.在函数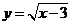 中,自变量
中,自变量 的取值范围是
的取值范围是
A.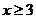 B.
B.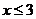 C.
C.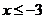 D.
D.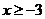
4,如图1,BC平分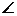 ABD,AB//CD,点E在CD的延长线上。若
ABD,AB//CD,点E在CD的延长线上。若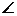 C=28°,则
C=28°,则 BDE的度数为
BDE的度数为
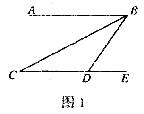
A.28° B.56° C.62° D.84°
5.某学校课外兴趣小组为了了解所在学校的学生对体育运动的爱好情况,设计了四种不同的抽样调查方案,你认为比较合理的是
A.在图书馆随机选择50名女生 B.在运动场随机选择50名男生
C.在校园内随机选择50名学生 D.在八年级学牛中随机选择50名学生
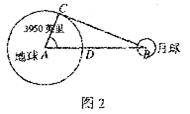
5.某资料中曾记载了一种计算地球与月球之间的距离的方法:如图2,假设赤道上一点D在AB上, ACB为直角,可以测量A的度数,则AB等于
ACB为直角,可以测量A的度数,则AB等于
A.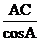 B.
B.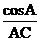 C.
C.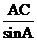 D.
D.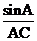
7.小贝与两位同学进行乒乓球比赛,用“手心、手背”游戏确定出场顺序。假设每人每次出手心、手背的可能性相同,若有一人与另外两人不同,则此人最后出场。三人同时出手一次。小贝最后出场比赛的概率为
A.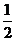 B.
B.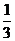 C.
C.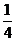 D.
D.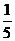
8.北京奥运会金牌创造性地将白玉圆环嵌在其中,这一设计不仅是对获胜者的礼赞,也形象地诠释了中华民族自古以来以“玉”比“德”的价值观。若白玉圆环面积与整个金牌面积的比值为k,则下列各数与k最接近的是

A.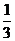 B.
B.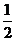 C.
C.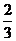 D.
D.
二、填空题(本题共l6分,每小题4分)
9.若关于 的一元二次方程
的一元二次方程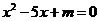 有实数根,则
有实数根,则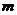 的取值范围是
。
的取值范围是
。
10.若圆锥的底面半径为6cm,高为8cm,则这个圆锥的侧面积是 cm3。
11.用“#”定义一种运算:对于任意实数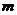 、
、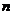 和抛物线
和抛物线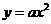 ,当
,当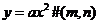 后都可得到
后都可得到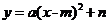 。例如:当
。例如:当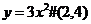 后得到
后得到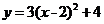 。若函数
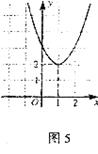
。若函数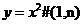 后得到了新的函数(如图5所示)则= 。
后得到了新的函数(如图5所示)则= 。
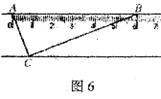
12.已知:如图6,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上。若 ACB=
ACB=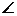 ADB=90°,则C、D两点之间的距离为 。
ADB=90°,则C、D两点之间的距离为 。
三,解答题(本题共30分,每小题5分。)
13.计算: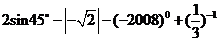
14.解不等式组: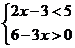
15.解分式方程: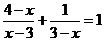
16.先化简,再求值: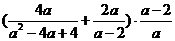
其中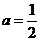 。
。
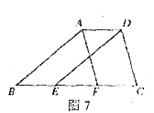
17.已知:如图7,在四边形ABCD中,点E、F在BC上,AB//DE,BE=FC,AB=DE。求证:AF=DC。
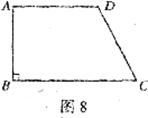
18.已知:如图8,梯形ABCD中,AD//BC,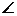 B=90°,AD=DC=2,
B=90°,AD=DC=2,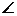 ADC=120°。求梯形ABCD的周长。
ADC=120°。求梯形ABCD的周长。
四、解答题(本题共20分,第19题4分,第20题5分,第21题6分,第22题5分。)
19.在平面直角坐标系 中,直线
中,直线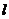 与直线
与直线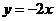 关于
关于 轴对称,直线
轴对称,直线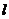 与反比例函数
与反比例函数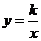 的图像的一个交点为
的图像的一个交点为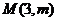 ,试确定反比例函数的解析式。
,试确定反比例函数的解析式。
20.某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远。有关数据整理如下:
立定跳远成绩(分)
学生人数(人)
10
m
9
16
8
4
7
n
6
2
5
2
合计
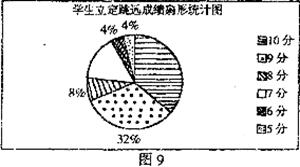
(1)依据图表信息,可知此次调查的样本容量为 ;
(2)在扇形统计图(如图9)中表示立定跳远成绩为8分的扇形圆心角的度数为 。(精确到1°);
(3)已知测试成绩为10分的学生比成绩为7分的学生多10人,求m和n的值。
21.如图10,AB经过⊙O的圆心,弦DF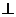 AB于E,BF切⊙O于F,⊙O的半径为2。
AB于E,BF切⊙O于F,⊙O的半径为2。
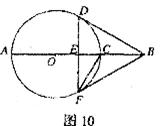
(1)求证:BD与⊙O相切;
(2)若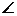 ABD=
ABD=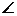 DFC,求DF的长。
DFC,求DF的长。
22.例,如图11一①,平面直角坐标系中有点B(2,3)和C(5,4):求△OBC的面积。
解:过点B作BD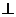
 轴于D,过点C作CE
轴于D,过点C作CE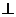
 轴于E。依题意,可得
轴于E。依题意,可得
S△OBC=S梯形BDEC+ S△OBD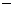 S△OCE
S△OCE
=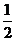 (BD+CE)(OE-OD)+
(BD+CE)(OE-OD)+ 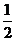 OD
OD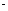 BD
BD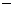
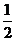 OE
OE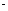 CE
CE
=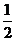
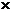 (3+4)
(3+4) 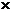 (5-2)+
(5-2)+ 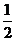
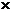 5
5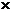 4=3.5
4=3.5
∴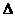 OBC的面积为3.5。
OBC的面积为3.5。
(1)如图11一②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上。仿照例题的解法,求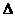 OBC的面积(用x1,y1、x2,y2的代数式表示);
OBC的面积(用x1,y1、x2,y2的代数式表示);
(2)如图11一③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积。
五、解答题(本题共22分,第23题6分,第24题8分,第25题8分。)
24.已知:点P为线段AB上的动点(与A、B两点不重合)。在同一平面内,把线段AP、BP分别折成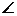 CDP、
CDP、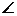 EFP,其中
EFP,其中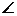 CDP=
CDP=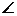 EFP=90°,且D、P、F三点共线。如图15所示。
EFP=90°,且D、P、F三点共线。如图15所示。
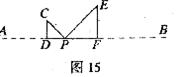
(1)若△CDP、△EFP均为等腰三角形,且DF=2,求AB的长;
(2)若AB=12,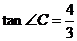 ,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值。
,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值。
25.在平面直角坐标系 ,已知直线
,已知直线 交
交 于点C,交
于点C,交 轴于点A。等腰直角三角板OBD的顶点D与点G重合,如图l6一①所示.把三角板绕着点O顺时针旋转,旋转角度为
轴于点A。等腰直角三角板OBD的顶点D与点G重合,如图l6一①所示.把三角板绕着点O顺时针旋转,旋转角度为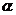 (
( ),使B点恰好落在AC上的
),使B点恰好落在AC上的 。如图l6一②所示。
。如图l6一②所示。


(1)求图l6一①中的点B的坐标;
(2)求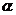 的值;
的值;
(3)若二次函数 的图像经过(1)中的点B,判断点
的图像经过(1)中的点B,判断点 是否在这条抛物线上,并说明理由。
是否在这条抛物线上,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com