
2007-2008学年度北京市宣武区第一学期期末测评
九年级数学
第Ⅰ卷 (共60分)
一、选择题(本大题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一项是符合题意的)
1.若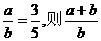 的值 ( )
的值 ( )
A. B.
B.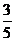 C.
C. D.
D.
2.抛物线 的对称轴是 ( )
的对称轴是 ( )
A.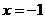 B.
B.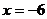 C.
C.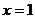 D.
D.
3.在平面直角坐标系中,已知点 等于 ( )
等于 ( )
A.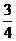 B.―
B.―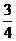 C.
C.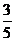 D.
D.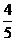
4.两个圆的半径分别是
A.外离 B.相交
C.内切 D.外切
5.如图,P是Rt△ABC的斜边BC上 异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )条。

A.1 B.2
C.3 D.4
6.如图,点A是反比例函数图象上的一点,自点A向y轴作垂线,垂足为T,已知 ,则此函数的表达式为( )
,则此函数的表达式为( )
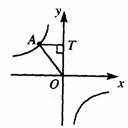
A.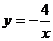 B.
B.
C. D.
D.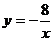
7.在元旦游园晚会上有一个闯关活动:将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关。那么一次过关的概率是 ( )
A.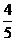 B.
B. C.
C.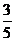 D.
D.
8.由于被墨水污染,一道数学题仅能见到如下文字:
已知二次函数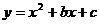 的图象过点(1,0),……求证这个二次函数的图象关于直线
的图象过点(1,0),……求证这个二次函数的图象关于直线 对称,根据现有信息,题中的二次函数不具有的性质是 ( )
对称,根据现有信息,题中的二次函数不具有的性质是 ( )
A.过点(3,0) B.顶点是(2,―2)
C.在x轴上截得的线段长是2 D.与y轴的交点是(0,3)
二、填空题(本大题共4小题,每小题4分,共16分,把答案写在题中横线上)
9.已知点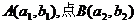 两点都在反比例函数
两点都在反比例函数 ,那么b1 b2。
,那么b1 b2。
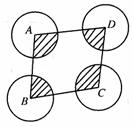
10.如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次联结四个圆心得到四边形ABCD,则图开中四个扇形(阴影部分)的面积之和是 。(结果中保留π)
|