|
试题详情
试题详情
三.解答题(每题5分,共20分) 15.化简 试题详情
16.如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数。 试题详情
试题详情
试题详情
si n45°=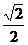 ,cos45°= ,cos45°=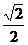 ,tan45°=1) ,tan45°=1) 试题详情
试题详情
18.某市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间宿舍.如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人? 试题详情
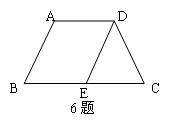
四.解答题(每题6分,共12分) 19.如图,用三个全等的菱形ABGH,、BCFG、CDEF拼成平行四边形ADEH,连结AE与BG、CF分别交于P、Q。 (1)若AB= 6 ,求线段BP的长; (2)观察图形,是否有三角形与△ACQ全等?并证明你的结论. 试题详情
试题详情
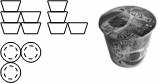
20.阿明通过对某地区2003年至2005年快餐公司发展情况的调查,制成了该地区快餐公司个数情况的扇形图和快餐公司盒饭年销量的平均数情况条形图。 根据所提供信息回答下列问题: (1)该地区最多的一年的年销量是多少万盒? (2)若每盒盒饭平均8元,上缴税为10%,试在右下图画出该地区2003至2005年仅快餐公司上缴税的折线图。 试题详情
 五.解答题(每题6分,共12分) 五.解答题(每题6分,共12分) 试题详情
21.在如图的方格纸中,每个小正方形的边长都为l,△ABC与△A1B1C1构成的图形是中心对称图形。 (l)画出此中心对称图形的对称中心O; (2)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2; (3)要使△A2B2C2与△CC1C2垂合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(不要求证明) 试题详情
试题详情
22.如图,直线y= 分别与x轴、 y轴交于B、A两点 分别与x轴、 y轴交于B、A两点 (1)求B、A两点的坐标; (2)把△ABO以直线 AB为轴翻折,点O落在平面上的点C处,以 BC为一边作等边△BCD,求D点的坐标 试题详情

六.解答题(每题7分,共14分) 试题详情
23.桌面上放有4张卡片,正面分别标有数字1,2,3,4,这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍反面朝上放回洗匀,乙从中任意抽出一张,记下卡片上的数字,然后将这两数相加; (1)请用列表或画树状图的方法求两数和为5的概率; (2)若甲与乙按上述方式作游戏,当两数之和为5时,甲胜;反之则乙胜;若甲胜一次得12分,那么乙胜一次得多少分,这个游戏对双方才公平。 试题详情
24.某食品批发部准备用10000元从厂家购进一批出厂价分别为16元/箱和20元/箱的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元). (1)求所获销售利润y(元)与x(箱)之间的函数关系式; (2)根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少? 七.解答题(每题10分,共20分) 试题详情
25.第一象限内的点A在一反比例函数的图象上,过A作AB⊥ 轴,垂足为B,连AO,已知△AOB的面积为4。 轴,垂足为B,连AO,已知△AOB的面积为4。 (1)求反比例函数的解析式; 试题详情
(2)若点A的纵坐标为4,过点A的直线与 轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标; 轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标; 试题详情
(3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线 平移得到?若是,请说明由抛物线 平移得到?若是,请说明由抛物线 如何平移得到;若不是,请说明理由。 如何平移得到;若不是,请说明理由。 试题详情
试题详情
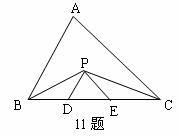
26.如图,菱形ABCD的边长为6 cm,∠DAB=60°,点M是边AD上一点,且DM= 2 cm,点E、F分别从A,C同时出发,以1 cm/s的速度分别沿边 AB、CB向点B运动,EM、CD的延长线相交于G,GF交AD于O.设运动时间为x(s),△CGF的面积为y( ) ) (1)求y与x之间的函数关系式; (2)当x为何值时,GF⊥AD? (3)是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为3∶7?若存在,求出此时x的值;若不存在,说明理由. 试题详情
试题详情
试题详情
| 
 B、
B、 C、
C、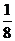 D、
D、
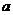 重合的是( )
重合的是( )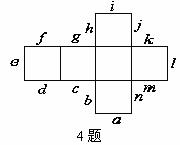
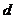 B、
B、 C、
C、 D、
D、
 B.
B. C.
C. D.
D.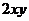
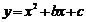 的部分图象如图所示,若y<0,则x的取值范围是 ( )
的部分图象如图所示,若y<0,则x的取值范围是 ( )
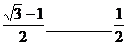

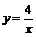 (x>0)的图象相交于A、B。设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形周长为
。
(x>0)的图象相交于A、B。设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形周长为
。