
2007-2008学年度淄川区第一学期期末考试
初三数学试题
亲爱的同学们:
这份试题将再次记录你的自信、沉着、智慧和收获,老师会一直投给你信任的目光。请你认真审题,看清要求,仔细答题.别忘了,还有5分的卷面分等你拿,祝你考出好成绩,为初三学年的期末数学学习画上圆满的句号!
一、精心选一选(本题共13小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,每小题3分,计39分)。
1.若分式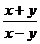 中的
中的 ,
, 的值都变为原来的3倍,则此分式的值
的值都变为原来的3倍,则此分式的值
(A)是原来的3倍 (B)不变
(C)是原来的 (D)是原来的
(D)是原来的
2.当 时,下列各式一定有意义的是
时,下列各式一定有意义的是
(A)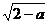 (B)
(B) (C)
(C) (D)
(D)
3.下列命题是真命题的为
(A)所有矩形都相似 (B)有一个角相等的三角形相似
(C)有一个角相等的等腰三角形相似 (D)任意两个等边三角形都相似
4.为了完成以下任务:(1)了解你们班同学周末时间是如何安排的;(2)了解某城市居民看某电视节目的收视率;(3)了解我国八年级学生的平均每天睡眠时间;(4)了解一大批电视机的产品合格率.其中既能采用抽样调查也能采用普查方式的有
(A)4件 (B)3件 (C)2件 (D)1件
5.已知△ABC的三边长分别为
(A)
6.化简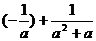 的结果是
的结果是
(A)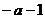 (B)
(B)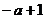 (C)
(C)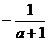 (D)
(D)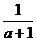
7.小明同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是
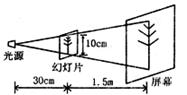
(A)
8.下列计算错误的是
(A)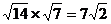 (B)
(B)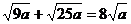
(C)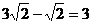 (D)
(D)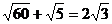
9.某校现有人数1800人,为了增强学生的法律意识,学校组织全体学生进行了一次普法考试。现抽取部分测试成绩(得分取整数)作为样本,进行整理后分成五组,并绘制成频数分布直方图。根据图中提供的信息,下列判断不正确的是
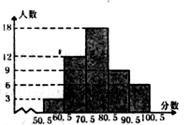
(A)样本中50.5~70.5这一分数段的频率是0.25
(B)样本容量是48
(C)估计本次测试全校在90分以上的学生约有225人
(D)样本的中位数落在70.5~80.5这一分数段内
10.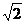 的同类二次根式是
的同类二次根式是
(A)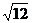 (B)
(B)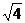 (C)
(C)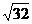 (D)
(D)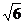
11.如图所示,若∠3=l10°,那么 等于
等于
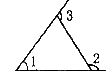
(A)55° (B)70° (C)90° (D)110°
班级
参加人数
中位数
平均数
方差
一班
40
148
150
280
二班
40
151
150
110
①一、二两班学生成绩的平均水平相同:
②一班的优秀人数比二班的优秀人数少(每分钟跳绳的次数≥150为优秀);
③一班的成绩较为稳定。上述结论正确的是
(A)①②③ (B)①② (C)①③ (D)②③
12.某校八年级一、二班举行跳绳比赛,参加学生每分钟跳绳的成绩统计如下表所示:某同学根据上表分析得出如下结论:
13.王强从A处沿北偏东60°的方向到达B处,又从B处沿南偏西25°的方向到达C处,则王强两次行进路线的夹角为
(A)145° (B)95° (C)85° (D)35°
二、细心填一填(本题共8小题,满分24分,只要求填写最后结果,每小题填对得3分)。
14.当 时,
时, 与
与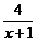 相等。
相等。
15.计算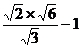 的结果是 。
的结果是 。
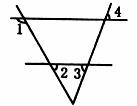
16.如图所示,∠1+∠2=180°,若∠3=47°,则∠4= 度。
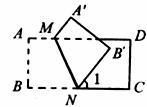
17.如图,在矩形ABCD中,将四边形ABNM沿MN折叠,若∠1=50°,则∠AMN= 度。
18.将50个数据分成三组,第一组与第三组的频数之和为35,则第二的频率是 。
19.若一组数据:1,2, ,3,4的平均数是3,则这组数据的方差是 。
,3,4的平均数是3,则这组数据的方差是 。
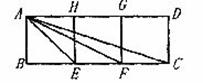
20.如图所示,ABEH,HEFG,GFCD都是正方形,则△AEC相似于 。
21.若 为整数,且
为整数,且 满足
满足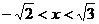 ,则
,则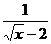 的值为 。
的值为 。
三、耐心做一做,相信你能写出正确的解答过程(共57分,注意审题要细心,书写要规范和解答要完整)
22.(本题满分24分,每小题6分)完成下列各题。
(1)化简: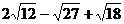 (2)化简:
(2)化简: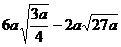
(3)计算: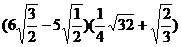
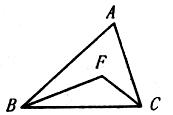
(4)如图,在△ABC中,BF平分∠ABC,CF平分∠ACB, A=50°,求∠BFC的大小。
23.(本题满分7分)请将下面证明中每一步的理由填在相应的扩号内。
已知:如图,CD⊥AB,GF⊥AB,∠l=∠2。求证:DE∥BC。
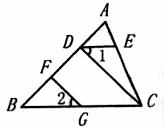
证明:∵CD⊥ AB, ( )
∴∠1+∠ADE=90°; ( )
∵GF⊥AB, ( )
∴∠2+∠B=90°; ( )
又∵∠1=∠2, ( )
∴∠ADE=∠B; ( )
∴DE∥BC ( )
24.(本题满分8分)
某中学为促进课堂教学,提高教学质量,对八年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查。根据收回的问卷,学校绘制了“频事分布表”和“频数分布直方图”。请你根据图、表中的信息,解决下列问题:
代号
教学方式
最喜欢的频数
频率
l
老师讲,学生听
20
0.15
4
分组讨论,解决问题
0.25
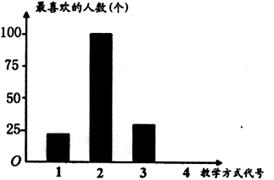
(1)补全频率分布表;
(2)在“频数分布直方图”中,将代号为“4”的部分补充完整;
(3)你最喜欢哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由。(字数在20字以内)
25.(本题满分9分)
甲、乙两工程队分别承担一条 千米,另一半时间每天维修公路
千米,另一半时间每天维修公路 千米。乙队维修前
千米。乙队维修前 千米;维修后
千米;维修后 千米(
千米(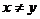 )。
)。
(1)求甲、乙两工程队完成任务所需要的时间(用含 ,
, 的代数式表示);
的代数式表示);
(2)问甲、乙两工程队哪个队先完成任务?为什么?
26.(本题满分9分)
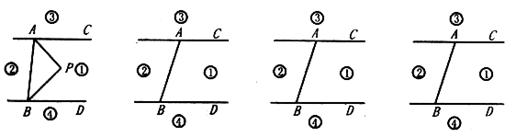
如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①,②,③,④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连接PA,PB,构成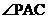 ,∠APB,∠PBD三个角。(提示:有公共顶点的两条重合的射线所组成的角是0°角)
,∠APB,∠PBD三个角。(提示:有公共顶点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠APB,∠PAC,∠PBD之间的关系,并写出动点P的具体位置和相应的结论,选择其中一种结论加以证明。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com