
2008年济南市高中阶段学校招生考试
数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.
第I卷(选择题 共48分)
一、选择题:本大题共12个小题.每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.-2的绝对值是( )
A.2 B.-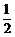 D.
D.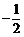
2.下列计算正确的是( )
A.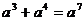 B.
B.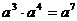 C.
C.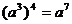 D.
D.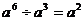
3.下面简单几何体的主视图是( )

4.国家游泳中心――“水立方”是2008年北京奥运会标志性建筑物之一,其工程占地面积为62828平方米,将62828用科学记数法表示是(保留三个有效数字) ( )
A.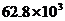 B.
B.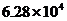
C.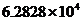 D.
D.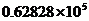
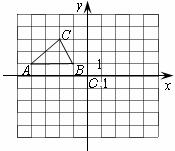
5.已知 在平面直角坐标系中的位置如图所示,将
在平面直角坐标系中的位置如图所示,将 向右平移6个单位,则平移后A点的坐标是( )
向右平移6个单位,则平移后A点的坐标是( )
A.(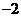 ,1) B.(2,1)
,1) B.(2,1)  C.(2,
C.(2,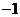 ) D.(
) D.(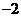 ,
,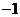 )
)
6.四川省汶川发生大地震后,全国人民“众志成城,抗震救灾”,积极开展捐款捐物献爱心活动.下表是我市某中学初一?八班50名同学捐款情况统计表:
捐款数(元)
10
15
20
30
50
60
70
80
90
100
人 数(人)
3
10
10
15
5
2
1
1
1
2
根据表中提供的信息,这50名同学捐款数的众数是( )
A.15 B.
7.如图:点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,若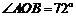 ,则
,则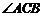 的度数是( )
的度数是( )
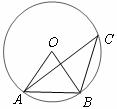
A.18° B.30° C.36° D.72°
8.如果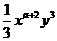 与
与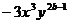 是同类项,那么a、b的值分别是( )
是同类项,那么a、b的值分别是( )
A.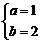 B.
B.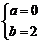 C.
C.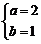 D.
D.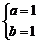
9.“迎奥运,我为先”联欢会上,班长准备了若干张相同的卡片,上面写的是联欢会上同学们要回答的问题.联欢会开始后,班长问小明:你能设计一个方案,估计联欢会共准备了多少张卡片?小明用20张空白卡片(与写有问题的卡片相同),和全部写有问题的卡片洗匀,从中随机抽取10张,发现有2张空白卡片,马上正确估计出了写有问题卡片的数目,小明估计的数目是( )
A.60张 B.80张 C.90张 D.110张
10.关于x的一元二次方程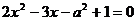 的一个根为2,则a的值是( )
的一个根为2,则a的值是( )
A.1 B. C.
C. D.
D.
11.济南市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )

A.4小时 B.4.4小时 C.4.8小时 D.5小时
12.如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)
(k≠0)
与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )

A. B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题 共72分)
二、填空题:本大题共5个小题.每小题3分,共15分.把答案填在题中横线上.
13.当 时,代数式
时,代数式 的值是 .
的值是 .
14.分解因式: = .
= .
15.如图,在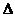 ABC中,EF为
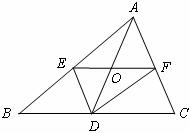
ABC中,EF为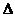 ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连接DE、DF,要使四边形AEDF为平行四边形,需要添加条件
ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连接DE、DF,要使四边形AEDF为平行四边形,需要添加条件
.(只添加一个条件)
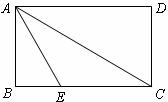
16.如图:矩形纸片ABCD,AB=2,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好落在AC上,则AC的长是 .
17.数学的美无处不在.数学家们研究发现,弹拨琴弦发出声音的音调高低,取决于弦的长度,绷得一样紧的几根弦,如果长度的比能够表示成整数的比,发出的声音就比较和谐.例如,三根弦长度之比是15:12:10,把它们绷得一样紧,用同样的力弹拨,它们将分别发出很调和的乐声do、mi、so.研究15、12、10这三个数的倒数发现: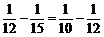 .我们称15、12、10这三个数为一组调和数.现有一组调和数:x、5、3(x>5),则x的值是 .
.我们称15、12、10这三个数为一组调和数.现有一组调和数:x、5、3(x>5),则x的值是 .
三、解答题:本大题共7个小题.共57分.解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分7分)
(1)解方程: .
.
(2)解不等式组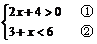 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
19.(本小题满分7分)
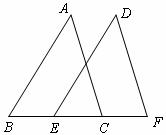
(1)已知:如图,AB∥DE,AC∥DF,BE=CF. 求证:AB=DE.
(2)已知:如图,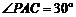 ,在射线AC上顺次截取AD=
,在射线AC上顺次截取AD=
20.(本小题满分8分)
完全相同的4个小球,上面分别标有数字1、-1、2、-2,将其放入一个不透明的盒子中摇匀,再从中随机摸球两次(第一次摸出球后放回摇匀).把第一次、第二次摸到的球上标有的数字分别记作m、n,以m、n分别作为一个点的横坐标与纵坐标,求点(m,n)不在第二象限的概率.(用树状图或列表法求解)
21.(本小题满分8分)
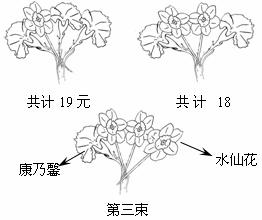
教师节来临之际,群群所在的班级准备向每位辛勤工作的教师献一束鲜花,每束由4支鲜花包装而成,其中有象征母爱的康乃馨和象征尊敬的水仙花两种鲜花,同一种鲜花每支的价格相同.请你根据第一、二束鲜花提供的信息,求出第三束鲜花的价格.
22.(本小题满分9分)
某大草原上有一条笔直的公路,在紧靠公路相距
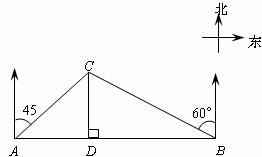
(1)求牧民区到公路的最短距离CD.
(2)你认为甲医疗队设计的两种救助方案,哪一种方案比较合理?并说明理由.
(结果精确到0.1.参考数据: 取1.73,
取1.73,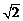 取1.41)
取1.41)
23.(本小题满分9分)
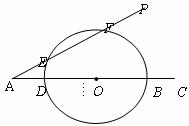
已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.
相交于点P.
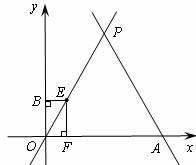
(1)求点P的坐标.
(2)请判断 的形状并说明理由.
的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值.
24.(本小题满分9分)
已知:抛物线 (a≠0),顶点C (1,
(a≠0),顶点C (1, ),与x轴交于A、B两点,
),与x轴交于A、B两点, .
.

(1)求这条抛物线的解析式.
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断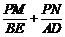 是否为定值? 若是,请求出此定值;若不是,请说明理由.
是否为定值? 若是,请求出此定值;若不是,请说明理由.
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断 是否成立.若成立,请给出证明;若不成立,请说明理由.
是否成立.若成立,请给出证明;若不成立,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com