
2008年泰安市高中段学校招生考试
数学试卷
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1. 的相反数是( )
的相反数是( )
A. B.
B. C.
C. D.
D.
2.如图是由相同小正方体组成的立体图形,它的左视图为( )


3.下列运算正确的是( )
A. B.
B. C.
C. D.
D.
4.如图,下列条件之一能使平行四边形ABCD是菱形的为( )

① ②
② ③
③ ④
④
A.①③ B.②③ C.③④ D.①②③
5.分式方程 的解是( )
的解是( )
A. B.
B. C.
C. D.
D.
6.如图,在⊙O中, 的度数为
的度数为 是
是 上一点,
上一点, 是
是 上不同的两点(不与
上不同的两点(不与 两点重合),则
两点重合),则 的度数为( )
的度数为( )

A. B.
B. C.
C. D.
D.
7.在0,1,2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为( )
A. B.
B. C.
C. D.
D.
8.直角三角形纸片的两直角边长分别为6,8,现将 如图那样折叠,使点
如图那样折叠,使点 与点
与点 重合,折痕为
重合,折痕为 ,则
,则 的值是( )
的值是( )

A. B.
B. C.
C. D.
D.
9.函数 的图象如图所示,下列对该函数性质的论断不可能正确的是( )
的图象如图所示,下列对该函数性质的论断不可能正确的是( )

A.该函数的图象是中心对称图形
B.当 时,该函数在
时,该函数在 时取得最小值2
时取得最小值2
C.在每个象限内, 的值随
的值随 值的增大而减小
值的增大而减小
D. 的值不可能为1
的值不可能为1
10.在同一直角坐标系中,函数 和
和 (
( 是常数,且
是常数,且 )的图象可能是(
)
)的图象可能是(
)

11.如图,圆锥的侧面积恰好等于其底面积的2倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )

A. B.
B. C.
C. D.
D.
12.如图所示是二次函数 的图象在
的图象在 轴上方的一部分,对于这段图象与
轴上方的一部分,对于这段图象与 轴所围成的阴影部分的面积,你认为与其最接近的值是( )
轴所围成的阴影部分的面积,你认为与其最接近的值是( )

A.4 B. C.
C. D.
D.
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共7小题,满分21分.只要求填写结果,每小题填对得3分)
13.计算 的结果是 .
的结果是 .
14.将 分解因式的结果是 .
分解因式的结果是 .
15.在如图所示的单位正方形网格中,将 向右平移3个单位后得到
向右平移3个单位后得到 (其中
(其中 的对应点分别为
的对应点分别为 ),则
),则 的度数是 .
的度数是 .

17.若等腰梯形 的上、下底之和为4,并且两条对角线所夹锐角为
的上、下底之和为4,并且两条对角线所夹锐角为 ,则该等腰梯形的面积为
(结果保留根号的形式).
,则该等腰梯形的面积为
(结果保留根号的形式).
18.四边形 的对角线
的对角线 的长分别为
的长分别为 ,可以证明当
,可以证明当 时(如图1),四边形
时(如图1),四边形 的面积
的面积 ,那么当
,那么当 所夹的锐角为
所夹的锐角为 时(如图2),四边形
时(如图2),四边形 的面积
的面积 .(用含
.(用含 的式子表示)
的式子表示)

19.如图,将边长为1的正三角形 沿
沿 轴正方向连续翻转2008次,点
轴正方向连续翻转2008次,点 依次落在点
依次落在点 的位置,则点
的位置,则点 的横坐标为 .
的横坐标为 .

三、解答题(本大题共7小题,满分63分.解答要写出必要的文字说明、证明过程或推演步骤)
20.(本小题满分8分)
(1)先化简,再求值: ,其中
,其中 .
.
(2)用配方法解方程: .
.
21.(本小题满分7分)
为了解某品牌A,B两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:
月份
一月
二月
三月
四月
五月
六月
七月
A型销售量(单位:台)
10
14
17
16
13
14
14
B型销售量(单位:台)
6
10
14
15
16
17
20
(1)完成下表(结果精确到0.1):
平均数
中位数
方差
A型销售量
14
B型销售量
14
18.6
(2)请你根据七个月的销售情况在图中绘制成折线统计图,并依据折线图的变化趋势,对专卖店今后的进货情况提出建议(字数控制在20~50字).

22.(本小题满分9分)
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形, 在同一条直线上,连结
在同一条直线上,连结 .
.

(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: .
.
23.(本小题满分9分)
某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8∶20~12∶00,下午14∶00~16∶00,每天25元;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件)
生产乙产品件数(件)
所用总时间(分)
10
10
350
30
20
850
信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
24.(本小题满分10分)
如图所示, 是直角三角形,
是直角三角形, ,以
,以 为直径的⊙O交
为直径的⊙O交 于点
于点 ,点
,点 是
是 边的中点,连结
边的中点,连结 .
.

(1)求证: 与⊙O相切;
与⊙O相切;
(2)若⊙O的半径为 ,
, ,求
,求 .
.
25.(本小题满分10分)
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数 (亩)与补贴数额
(亩)与补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益 (元)会相应降低,且
(元)会相应降低,且 与
与 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.

(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数 和每亩蔬菜的收益
和每亩蔬菜的收益 与政府补贴数额
与政府补贴数额 之间的函数关系式;
之间的函数关系式;
(3)要使全市这种蔬菜的总收益 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额 定为多少?并求出总收益
定为多少?并求出总收益 的最大值.
的最大值.
26.(本小题满分10分)
在等边 中,点
中,点 为
为 上一点,连结
上一点,连结 ,直线
,直线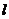 与
与 分别相交于点
分别相交于点 ,且
,且 .
.

(1)如图1,写出图中所有与 相似的三角形,并选择其中一对给予证明;
相似的三角形,并选择其中一对给予证明;
(2)若直线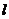 向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当 满足什么条件时(其它条件不变),
满足什么条件时(其它条件不变), ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com