1．下列代数式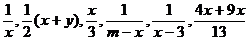中，是分式的有(    )

A．2个       B．3个              C．4个              D．5个

2．如果分式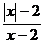的值为零，那么的值为(    )

A．2           B．－2              C．土2              D．0

3．在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中，首次使用了我国科研人员自主研制的强度为4．6×10⁸帕的钢材，那么4．6×10⁸的原数为(    )

A．4 600 000      B．46 000 000             C．460 000 000    D．4 600 000 000

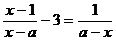4．已知关于的方程：的解是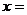3，则a的值为(    )

A．3                 B．－3              C．2                  D．－2

5．如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E。已知PE=3，则点P到AB的距离是(    )

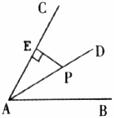
A．3                 B．4                  C 5                D．6

6．如图，△ABC和△DCB中，已知∠A=∠D，则下列条件中，不能判定△ABC≌△DCB的是(    )

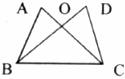
A．OB=OC        B．∠ABC=∠DCB     C．∠ACB=∠DBC      D．AB=CD

7．点P在第二象限内，P到轴的距离是4，到y轴的距离是3，那么点P关于轴对称点的坐标为(    )

A．(－4，3)      B．(－3，－4)    C．(－3，4)      D．(3，－4)

8．如果函数和的图象交于点P，那么点P应该位于(    )

A．第一象限       B．第二象限              C．第三象限              D．第四象限

9．如图，已知AC和BD相交于O点，AD//BC，AD=BC，过O点作一直线分别交AD、BC于点E、F，则下列结论：①OA=OC②OE=OF(3)AE=CF④OB=OD，其中成立的个数是(   )

A．1个       B．2个              C．3个              D．4个

10．如图，直线与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△AO’B’，则点B’的坐标是(    )

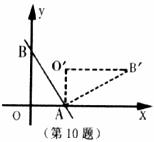
A．(3，4)          B．(4，5)                 C．(7，4)           D．(7，3)

11．如图，、分别是甲、乙两弹簧的长(cm)与所挂物体质量(kg)之间的函数关系的图像．设甲弹簧每挂1kg物体伸长的长度为，乙弹簧每挂1kg物体伸长的长度为cm，则与的大小关系(    )．

A．    B．              C．         D．不能确定

12．“五一”放假期间，某校八年级学生小明骑自行车到30千米的国家环境保护区进行“社会小调查”活动，小明出发30分钟后，小亮乘汽车出发，结果他们同时到达，已知汽车速度是自行车速度的2倍。则小明到达目的地用了(    )

A．2小时          B．1．5小时              C．1小时                  D．45分钟

13．计算：         

14．小明家距离学校m千米，骑自行车需要小时。一天小明从家出发迟了小时，如果他到达学校的时间和往常一样，那么他骑车的速度比原来提高        千米／小时。

    15．学习和研究《反比例函数的图象与性质》《一次函数的图象与性质》时，用到的数学思想方法有            、           、            (填3个即可)。

    16．在加油站，加油机显示器上显示的某一种油的单价为每升4．75元，总价从0元开始随着加油量的变化而变化，是总价y(元)与加油量(升)的函数关系式是                。

    17．用“如果……那么……”形式写出命题“平行于同一条直线的两条直线平行”的逆命题。                                                                        

    18．某市在旧城改造过程中，需要整修一段全长2400m的道路．为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20％，结果提前8小时完成任务。求原计划每小时修路的长度，若设原计划每小时修路m，则根据题意可得方程                

19．本题满分10分

    (1)先化简再求值：，其中。

    (2)解方程：解方程．

20．本题满分8分

(1)如图已知∠ABC，请你用直尺和圆规，作一个角，使它等于2∠ABC。

(要求：用尺规作图，不必写你是如何作的，但是要保留作图时留下的作图痕迹)

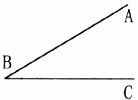
    (2)如图已知△ABC，请你用直尺和圆规作图，作一个三角，使它和△ABC全等。

    (要求：用尺规作图，保留作图时留下的作图痕迹，写出作法)

21．(本小题9分)

已知反比例函数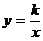的图象与一次函数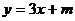的图象相交于点A(1，5)。

(1)求这两个函数的解析式；

(2)在同一平面直角坐标系内，画出一次函数和反比例函数图象

(3)若一次函数的图象与轴交于点B，求△ABO的面积

22．(本题满分8分)

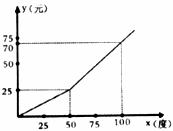
为缓解用电紧张矛盾，某电力公司特制定了新的用电收费标准，每月用电量(度)与应付电费y(元)的关系如图所示．

    (1)根据图象，请分别求出当0≤≤50和>50时，y与的函数关系式．

    (2)请回答：

    当每月用电量不超过50度时，收费标准是                  ；

    当每月用电量超过50度时，收费标准是                    。

23．(本小题满分7分)

如图，已知AB=DC，O是DB的中点，过O点的直线分别交BC和DA的延长线于E、F

    (1)求证△ABD≌△CDB

(2)求证：∠E=∠F

24．(本小题10分)

    注意：为了引导同学们学好数学，本题除了要求解决外，还要考查同学们对实际问题的分析方法。请你用平日学习的方法对下列实际问题进行分析：(提示：可用“列表分析法”、“读想分析法”、“线段图分析法”等，)

    实际问题：甲乙二人同时从张庄出发，步行15千米到李庄，甲的速度是乙的2倍，结果比乙早到半小时。问二人每小时各走几千米?

    (1)(5分)设乙每小时走千米，根据题意，运用你认为合适的方法进行分析。

    ①分析方法：(一种即可)

    ②等量关系：

(2)(5分)列出方程(组)，并求出问题的解。

25．(本题满分7分)

    如图：小刚站在河边的A点处，在河的对面(小刚的正北方向)的B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了20步到达一颗树C处，接着再向前走了20步到达D处，然后他左转90°直行，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他共走了100步。

    (1)根据题意，画出示意图；(在原图上即可)

    (2)如果小刚一步大约50厘米，估计小刚在点A处时他与电线塔的距离，并说明理由。

26．(本题满分8分)

某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利y(元)是1吨水的价格(元)的一次函数。

    (1)根据下表提供的数据，求y与之间的函数关系式；

    (2)当水价为每吨l0元时，该饮料厂若想获得2万元的利润，则至少需用水多少吨?(精确到个位)

    (3)请总结解决问题(1)的规律。