1．计算：4-（-2）=    .

2．分解因式：=     .

3.如图,已知AD//BC, ∠EAD=50 ^O,∠ACB=40 ^O,则∠BAC=      .

4．“凤凰号”火星探测器于去年从美国佛罗里达州卡纳维拉尔角发射,经过近10个月的时间,飞行了近680 000 000千米后到达火星。其中680 000 000千米用科学记数法可表示为   千米（保留三个有效数字）.

5．函数的自变量的取值范围是      .

6．已知⊙的半径为5┩，弦AB的长为8┩，则圆心到AB的距离为     ┩.

7．小红量得一个圆锥的母线长为15┩，底面圆的直径是6┩,它的侧面积为    ┩²(结果保留π).

8. 下面是一个三角形数阵：   

根据该数阵的规律,猜想第十行所有数的和是       .

9.图中的几何体的俯视图是    (     )

10．下列各式中与是同类二次根式的是  （    ）

A．2                        B．                       C．                   D．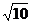

11．五边形的内角和为     （   ）

  A．360^O                 B．540^O                    C．720^O    　          D．900^O

12．下列说法正确的是　（    ）

A．检查地震灾区的食品质量应采取普查的方法

B．地震一周后,埋在废墟下的人员幸存的可能性很小,我们应放弃搜救行动

C．唐家山堰塞湖出现溃坝的概率是93%,说明该堰塞湖溃坝的可能性很大

D．我市发生地震的概率很小，则我市一定不会发生地震，我们不必学习相关知识

13．下面的函数是反比例函数的是   （  ）

    A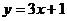．                                         B．  

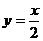 C．                                              D．

14．如图3，已知等边三角形ABC的边长为2，DE是它的中位线，则下面四个结论：　　　　　　　　　　　　　　　　

（1）DE=1，（2）AB边上的高为，（3）△CDE∽△CAB，（4）△CDE的面积与

△CAB面积之比为1：4.其中正确的有   （   ）

A．1个                B．2个                       C．3个                   D．4个

15．北京奥组委为了更好地传播奥运匹克知识，倡导奥林匹克精神，鼓励广大民众到现场观看精彩的比赛，小明一家积极响应,上网查得部分项目的门票价格如下：

项目

开幕式

篮球

足球

乒乓球

排球

跳水

体操

田径

射击

举重

羽毛球

闭幕式

价格

200

50

40

50

50

60

100

50

30

30

50

100

这些门票价格的中位数和众数分别是（   ）

　    A．50,  50　　　              B．67.5,  50　　　　 C．40,  30　　　　    D．50,  30

16．把抛物线向右平移2个单位，再向上平移1个单位，所得的抛物线的解析

式为   (    )

A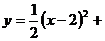．1                    B．1

      C．1                    D． 

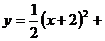17．计算：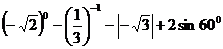

18．化简：

19．解不等式组            

20．在社会主义新农村建设中，县交通局决定对某乡的村级公路进行改造，由甲工程队单独施工，预计180天能完成。为了提前完成任务，改由甲、乙两个工程队同时施工，100天就能完成。试问：若由乙工程队单独施工，需要多少天才能完成任务？

五、 （本大题2个小题，每小题7分，满分14分）

21．如图，已知⊙O是△ABC的外接圆，AB为直径，若PA⊥AB，PO过AC的中点M，

求证：PC是⊙O的切线．

22．“无论多么大的困难除以13亿，都将是一个很小的困难”。在汶川特大地震发生后，我市光明中学全体学生积极参加了“同心协力，抗震救灾”活动，九年级甲班两位同学对本班捐款情况作了统计：全班50人共捐款900元，两位同学分别绘制了两幅不完整的统计图（注：每组含最小值，不含最大值）。

请你根据图中的信息，解答下列问题：

（1）       从图1中可以看出捐款金额在15-20元的人数有多少人？

（2）       从图2中可以看出捐款金额在25-30元的人数占全班人数的百分比是多少？

（3）       补全条形统计图，并计算扇形统计图的值；

（4）       全校共有1268人，请你估计全校学生捐款的总金额大约是多少元．

六、 （本大题2个小题，每小题8分，满分16分）

23．如图，在梯形ABCD中，若AB//DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．

  （1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少（注意：全等看成相似的特例）？

   （2）请你任选一组相似三角形，并给出证明．

上述过程说明：整数系数方程的整数解只可能是m的因数．

    例如：方程中－2的因数为±1和±2，将它们分别代入方程进行验证得：x=－2是该方程的整数解，－1、1、2不是方程的整数解．

解决问题：（1）根据上面的学习，请你确定方程的整数解只可能是哪几个整数？

（2）方程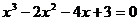是否有整数解？若有，请求出其整数解；若没有，请说明理由.

七、（本大题2个小题，每小题10分，满分20分）

25．如图，已知四边形ABCD是矩形，且MO=MD=4,MC=3.

(1)求直线BM的解析式;

(2)求过A、M、B三点的抛物线的解析式;

(3)在(2)中的抛物线上是否存在点P,使△PMB构成以BM为直角边的直角三角形?若没有,请说明理由;若有,则求出一个符合条件的P点的坐标.

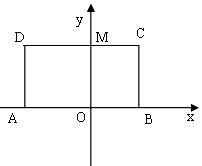
26． 如图，在直线上摆放有△ABC和直角梯形DEFG，且CD＝6┩；在△ABC中：∠C＝90^O，∠A＝30⁰，AB＝4┩；在直角梯形DEFG中：EF//DG，∠DGF＝90^O ,DG＝6┩，DE＝4┩，∠EDG＝60⁰。解答下列问题：

（1）旋转：将△ABC绕点C顺时针方向旋转90⁰，请你在图中作出旋转后的对应图形

△A₁B₁C，并求出AB₁的长度；

（2）翻折：将△A₁B₁C沿过点B₁且与直线垂直的直线翻折，得到翻折后的对应图形

△A₂B₁C₁，试判定四边形A₂B₁DE的形状？并说明理由；

（3）平移：将△A₂B₁C₁沿直线向右平移至△A₃B₂C₂，若设平移的距离为ｘ，△A₃B₂C₂与直角梯形重叠部分的面积为ｙ，当ｙ等于△ABC面积的一半时,ｘ的值是多少？