
2008年凉山州初中毕业、高中阶段招生统一考试
数学试卷
A卷(共100分)
第Ⅰ卷(选择题共30分)
一、选择题(每小题3分,共30分)
1.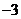 的相反数是(
)
的相反数是(
)
A.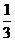 B.
B.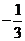 C.
C.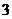 D.
D.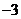
2.下列计算正确的是( )
A.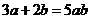 B.
B.
C.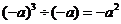 D.
D.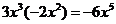
3.不等式组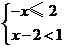 的解集在数轴上表示正确的是(
)
的解集在数轴上表示正确的是(
)

4.2007年搭载我国首颗探月卫星“嫦娥一号”的长征三号甲运载火箭在西昌卫星发射中心发射,并成功飞向距地球约
A.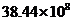 米 B.
米 B. 米 C.
米 C.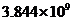 米 D.
米 D.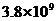 米
米
5.向上抛掷一枚硬币,落地后正面向上这一事件是( )
A.必然发生 B.不可能发生 C.可能发生也可能不发生 D.以上都对
6.如图,由四个棱长为“
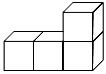
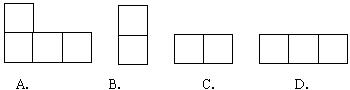
7.下列四个图形中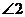 大于
大于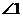 的是( )
的是( )

8.一个多边形的内角和与它的一个外角的和为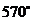 ,那么这个多边形的边数为(
)
,那么这个多边形的边数为(
)
A.5 B.
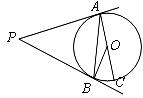
9.如图, 分别是⊙
分别是⊙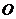 的切线,
的切线,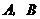 为切点,
为切点,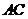 是⊙
是⊙ 的直径,已知
的直径,已知
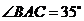 ,
,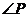 的度数为( )
的度数为( )
A.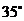 B.
B. C.
C.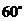 D.
D.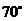
10.已知二次函数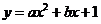 的大致图象如图所示,那么函数
的大致图象如图所示,那么函数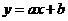 的图象不经过( )
的图象不经过( )

A.一象限 B.二象限 C.三象限 D.四象限
第Ⅱ卷(非选择题共70分)
二、填空题(每小题3分,共12分)
11.分解因式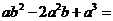 .
.
12.质检部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.02,那么,由此可以推断出生产此类产品,质量比较稳定的是 厂.
13.分式方程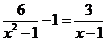 的解是
.
的解是
.
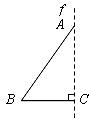
14.如图,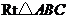 中
中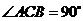 ,
,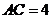 ,
, .将
.将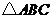 绕
绕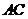 所在的直线
所在的直线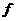 旋转一周得到一个旋转体,该旋转体的侧面积
旋转一周得到一个旋转体,该旋转体的侧面积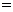 .(
.(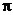 取3.14,结果保留两个有效数字)
取3.14,结果保留两个有效数字)
三、(15题18分,16、17各6分,共30分)
15.解答下列各题(每小题6分,共18分)
(1)计算:
(2)先化简再求值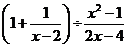 ,其中,
,其中,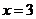 .
.
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:
得分(分)
10
9
8
7
人数(人)
5
8
4
3
问:①求这20位同学实验操作得分的众数、中位数.
②这20位同学实验操作得分的平均分是多少?
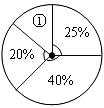
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
16.(6分)如图所示,图形(1)、(2)、(3)(4)分别由两个相同的正三角形、正方形、正五边形、正六边形组成.本题中我们探索各图形顶点、边数、区域三者之间的关系.(例我们规定如图(2)的顶点数为16;边数为24,像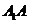 ,
,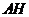 为边,
为边,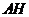 不能再算边,边与边不能重叠;区域数为9,它们由八个小三角形区域和中间区域
不能再算边,边与边不能重叠;区域数为9,它们由八个小三角形区域和中间区域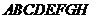 组成,它们相互独立.)
组成,它们相互独立.)
(1)每个图形中各有多少个顶点?多少条边?多少个区域?请将结果填入表格中.
图序
顶点个数(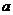 )
)
边数( )
)
区域(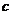 )
)
(1)
(2)
16
24
9
(3)
(4)
(2)根据(1)中的结论,写出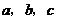 三者之间的关系表达式.
三者之间的关系表达式.
17.(6分)在平面直角坐标系中按下列要求作图.
(1)作出三象限中的小鱼关于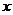 轴的对称图形;
轴的对称图形;
(2)将(1)中得到的图形再向右平移6个单位长度.
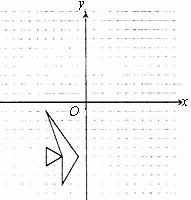
四、(18、19每小题6分,共12分)
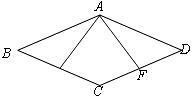
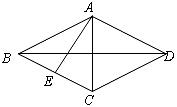
18.(6分)如图,点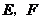 分别是菱形
分别是菱形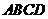 中
中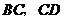 边上的点(
边上的点(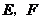 不与
不与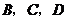 重合)在不连辅助线的情况下请添加一个条件,说明
重合)在不连辅助线的情况下请添加一个条件,说明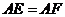 .
.
19.(6分)在不透明的口袋中装有大小、质地完全相同的分别标有数字1,2,3的三个小球,随机摸出一个小球(不放回),将小球上的数字作为一个两位数个位上的数字,然后再摸出一个小球将小球上的数字作为这个两位数十位上的数字(利用表格或树状图解答)
(1)能组成哪些两位数?
(2)小华同学的学号是12,有一次试验中他摸到自己学号的概率是多少?
五、(20题8分,21题8分,共16分)
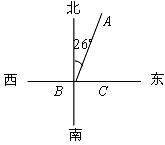
20.(8分)如图,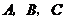 三个粮仓的位置如图所示,
三个粮仓的位置如图所示,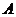 粮仓在
粮仓在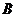 粮仓北偏东
粮仓北偏东 ,180千米处;
,180千米处;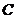 粮仓在
粮仓在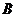 粮仓的正东方,
粮仓的正东方,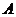 粮仓的正南方.已知
粮仓的正南方.已知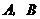 两个粮仓原有存粮共450吨,根据灾情需要,现从
两个粮仓原有存粮共450吨,根据灾情需要,现从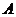 粮仓运出该粮仓存粮的
粮仓运出该粮仓存粮的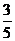 支援
支援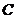 粮仓,从
粮仓,从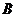 粮仓运出该粮仓存粮的
粮仓运出该粮仓存粮的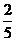 支援
支援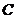 粮仓,这时
粮仓,这时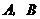 两处粮仓的存粮吨数相等.
两处粮仓的存粮吨数相等.
(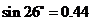 ,
,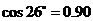 ,
,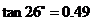 )
)
(1)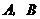 两处粮仓原有存粮各多少吨?
两处粮仓原有存粮各多少吨?
(2)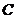 粮仓至少需要支援200吨粮食,问此调拨计划能满足
粮仓至少需要支援200吨粮食,问此调拨计划能满足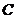 粮仓的需求吗?
粮仓的需求吗?
(3)由于气象条件恶劣,从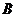 处出发到
处出发到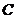 处的车队来回都限速以每小时35公里的速度匀速行驶,而司机小王的汽车油箱的油量最多可行驶4小时,那么小王在途中是否需要加油才能安全的回到
处的车队来回都限速以每小时35公里的速度匀速行驶,而司机小王的汽车油箱的油量最多可行驶4小时,那么小王在途中是否需要加油才能安全的回到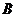 地?请你说明理由.
地?请你说明理由.
21.(8分)我州有一种可食用的野生菌,上市时,外商李经理按市场价格20元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160元,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设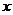 到后每千克该野生菌的市场价格为
到后每千克该野生菌的市场价格为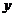 元,试写出
元,试写出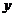 与
与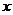 之间的函数关系式.
之间的函数关系式.
(2)若存放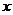 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为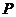 元,试写出
元,试写出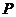 与
与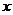 之间的函数关系式.
之间的函数关系式.
(3)李经理将这批野生菌存放多少天后出售可获得最大利润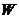 元?
元?
(利润=销售总额-收购成本-各种费用)
B卷(共20分)
六、填空:(每小题3分,共6分)
22.菱形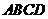 中,
中,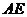 垂直平分
垂直平分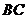 ,垂足为
,垂足为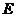 ,
, .那么,菱形
.那么,菱形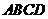 的面积是
,对角线
的面积是
,对角线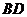 的长是 .
的长是 .
23.等腰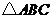 两边的长分别是一元二次方程
两边的长分别是一元二次方程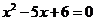 的两个解,则这个等腰三角形的周长是
.
的两个解,则这个等腰三角形的周长是
.
七、(24小题5分,25小题9分,共14分)
例:当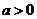 时,如
时,如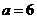 则
则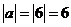 ,故此时
,故此时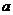 的绝对值是它本身
的绝对值是它本身
当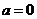 时,
时,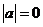 ,故此时
,故此时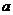 的绝对值是零
的绝对值是零
当 时,如
时,如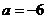 则
则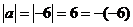 ,故此时
,故此时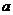 的绝对值是它的相反数
的绝对值是它的相反数
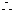 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
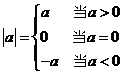
这种分析方法涌透了数学的分类讨论思想.
问:(1)请仿照例中的分类讨论的方法,分析二次根式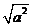 的各种展开的情况.
的各种展开的情况.
(2)猜想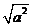 与
与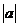 的大小关系.
的大小关系.
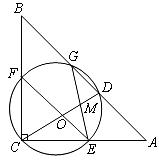
25.(9分)如图,在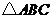 中
中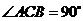 ,
,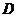 是
是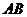 的中点,以
的中点,以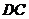 为直径的⊙
为直径的⊙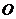 交
交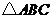 的三边,交点分别是
的三边,交点分别是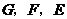 点.
点.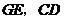 的交点为
的交点为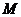 ,且
,且 ,
,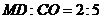 .
.
(1)求证: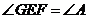 .
.
(2)求⊙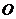 的直径
的直径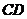 的长.
的长.
(3)若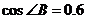 ,以
,以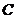 为坐标原点,
为坐标原点,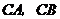 所在的直线分别为
所在的直线分别为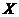 轴和
轴和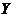 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线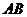 的函数表达式.
的函数表达式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com