
2008年乐山市高中阶段教育学校招生考试
数学试卷
第Ⅰ卷(选择题 36分)
一、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项符合题目要求。
1、|3.14-π|的值为
A、0 B、3.14-π C、π-3.14 D、0.14
2、如图,直线 相交于点O,OM⊥
相交于点O,OM⊥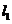 ,若
,若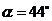 ,则β=
,则β=
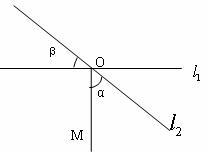
A、56° B、46° C、45° D、44°
3、已知二次根式 与
与 是同类二次根式,则的α值可以是
是同类二次根式,则的α值可以是
A、5 B、
4、如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网

A、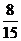 B、
B、  D、
D、
5、下列计算正确的是
A、 B、
B、 C、
C、 D、
D、
6、下列说法正确的是:
A、买一张彩票就中大奖是不可能事件
B、天气预报称:“明天下雨的概率是90%”,则明天一定会下雨
C、要了解夏季冷饮市场上冰淇淋的质量情况,可以采取抽样调查的方式进行
D、掷两枚普通的正方体骰子,点数之积是奇数与点数之积是偶数出现的机会相同
7、如图AD⊥CD,AB=13,BC=12,CD=3,AD=4,则sinB=

A、 B、
B、 C、
C、 D、
D、
8、函数 的自变量x的取值范围为
的自变量x的取值范围为
A、x≥-2 B、x>-2且x≠
9、
捐款数(元)
10
20
30
40
50
捐款人数(人)
8
17
16
2
2
则对全班捐款的45个数据,下列说法错误的是
A、中位数是30元 B、众数是20元 C、平均数是24元 D、极差是40元
10、如图(4),在直角坐标系中,四边形OABC为正方形,顶点A、C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为

A、(4,5) B、(-5,4) C、(-4,6) D、(-4,5)
11. 如图,在直角梯形ABCD中AD∥BC,点E是边CD的中点,若AB=AD+BC, BE= ,则梯形ABCD的面积为
,则梯形ABCD的面积为
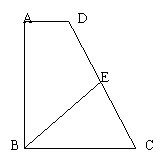

A、 B、
B、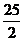 C、
C、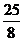 D、 25
D、 25
12、已知二次函数 的图象如图所示,令
的图象如图所示,令
 ,则
,则


A.M>0 B. M<
第Ⅱ卷(非选择题 共114分)
一. 填空题: 本大题共6小题,每小题3分,共计18分,把答案填在题中的横线上
13、如图,A、B两点在数轴上,点A对应的数为2,若线段AB的长为3,则点B对应的数为 。


14、为帮助“5?
15、计算: =
=
16、下图是一个几何体的三视图,根据图示,可计算出该几何体的侧面积为


17、下列函数:① ②
②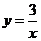 ③
③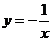 ④
④ 。当
。当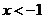 时,函数值y随自变量x的增大而减小的有
(填序号)
时,函数值y随自变量x的增大而减小的有
(填序号)
18、如图,在直角坐标系中,一直线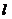 经过点
经过点 与x轴,y轴分别交于A、B两点,且MA=MB,则△ABO的内切圆⊙O1的半径
与x轴,y轴分别交于A、B两点,且MA=MB,则△ABO的内切圆⊙O1的半径 =
;若⊙O2与⊙O1、
=
;若⊙O2与⊙O1、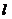 、y轴分别相切,⊙O3与⊙O2、
、y轴分别相切,⊙O3与⊙O2、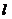 、y轴分别相切,…,按此规律,则⊙O2008的半径
、y轴分别相切,…,按此规律,则⊙O2008的半径 =
=

三、本大题共3小题,每小题9分,共27分
19、已知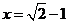 ,求代数式
,求代数式 的值
的值
20、若不等式组 的整数解是关于x的方程
的整数解是关于x的方程 的根,求a的值
的根,求a的值
21、如图,AC∥DE, BC∥EF,AC=DE
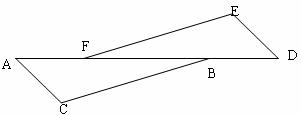
求证:AF=BD
22、如图,E、F分别是等腰△ABC的腰AB、AC的中点。
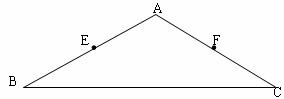
(1)用尺规在BC边上求作一点M,使四边形AEMF为菱形;(不写作法,保留作图痕迹)
(2)若AB=
23、解方程: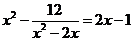
24、某校一课外活动小组为了解学生最喜欢的球类运动情况,随机抽查了样校九年级的200名学生,调查的结果如图所示,请根据该扇形统计图解答以下问题:
(1)求图中x的值
(2)求最喜欢乒乓球运动的学生人数
(3)若由3名最喜欢篮球运动的学生,1名最喜欢乒乓球运动的学生,1名最喜欢足球运动的学生组队外出参加一次联谊活,欲从中选出2人但任组长(不分正副),列出所有的可能情况,并求2人均是最喜欢篮球运动的学生的概率。



 五、本大题共2个小题,每小题9分,共18分,其中第25题为选作题
五、本大题共2个小题,每小题9分,共18分,其中第25题为选作题
25、从甲、乙两题中选做一题,如果两题都做,只以甲题计分。
题甲:如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE交AC于点F,BE的延长线交CD的延长线于点G。
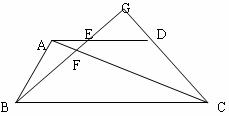
(1) 求证: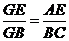
(2) 若GE=2,BF=3,求线段BF的长
题乙:下图是反比例函数 的图象,当-4≤x≤-1时,-4≤y≤-1
的图象,当-4≤x≤-1时,-4≤y≤-1

(1)求该反比例函数的解析式
(2)若M、N分别在反比例函数图象的两支上,请指出什么情况下线段MN最短(不需证明),并求出线段MN长度的取值范围
我选做的是
26、一家电脑公司推出一款新型电脑,投放市场以来3个月的利润情况如图所示,该图可以近似看作为抛物线的一部分,请结合图象,解答以下问题:
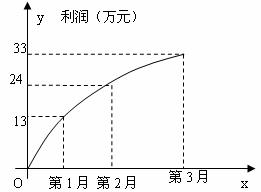
(1)求该抛物线对应的二次函数解析式
(2)该公司在经营此款电脑过程中,第几月的利润最大?最大利润是多少?
(3)若照此经营下去,请你结合所学的知识,对公司在此款电脑的经营状况(是否亏损?何时亏损?)作预测分析。
六、本大题共2小题,每小题12分,共24分
我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离;即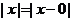 ,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
这个结论可以推广为 表示在数轴上
表示在数轴上 ,
, 对应点之间的距离;
对应点之间的距离;
例1 解方程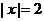 ,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
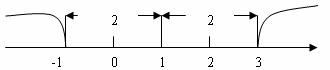
例2 解不等式 ,如图,在数轴上找出
,如图,在数轴上找出 的解,即到1的距离为2的点对应的数为-1、3,则
的解,即到1的距离为2的点对应的数为-1、3,则 的解为x<-1或x>3
的解为x<-1或x>3
例3 解方程 。由绝对值的几何意义知,该方程表示求在数轴上与1
。由绝对值的几何意义知,该方程表示求在数轴上与1
和-2的距离之和为5的点对应的x的值。在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3
(1)方程 的解为
的解为
(2)解不等式 ≥9;
≥9;
(3)若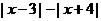 ≤a对任意的x都成立,求a的取值范围
≤a对任意的x都成立,求a的取值范围
28. 在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C
若C的坐标为(0,2),AB=5, A,B两点的横坐标XA,XB是关于X的方程
 的两根:
的两根:
(1) 求m,n的值
(2)
若∠ACB的平分线所在的直线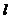 交x轴于点D,试求直线
交x轴于点D,试求直线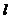 对应的一次函数的解析式
对应的一次函数的解析式
(3)过点D任作一直线 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com