
2008年北京市房山区中考二摸模拟练习(二)
数学试卷
一、选择题:
1. 的绝对值是
的绝对值是
A.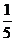 B.
B. C.
C.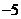 D.
D.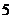
2.点P(-2,1) 关于原点对称的点的坐标是
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
3.下列运算中,正确的是
A.2x+5x=10x B.(ab2) 3=a3b6
C.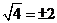
4.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到欢欢的概率是
A.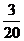 B.
B.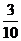 C.
C.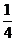 D.
D.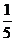
5. 如图,由几个小正方体组成的立体图形的俯视图是

6、如果圆锥的底面半径为
A.12πcm2 B.6πcm
7、如图,在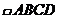 中,AC为对角线,
中,AC为对角线,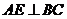 于E,
于E,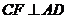 于F,则图中全等三角形共有
于F,则图中全等三角形共有
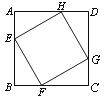
A.1对 B.2对 C.3对 D.4对
8、如图,正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE为x,则y关于x的函数图象大致是
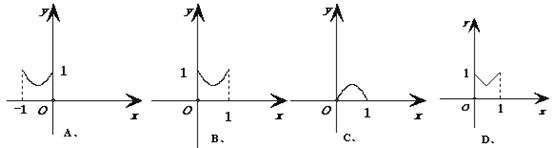
二、填空题(共4个小题,每小题4分,共16分)
9. 函数y=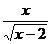 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
10、下表是某中学九年级(2)班环保小组的7名同学在回收废电池的活动中的统计结果
每人回收废电池的个数
12
13
15
15
10
8
11
请根据以上数据,回答下列问题:
7名学生回收废电池的个数的平均数是 ;众数是 .
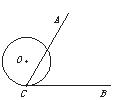
11.如图,∠ACB=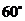 ,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为 .
,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为 .
12. 如图1是一种边长为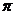 ).
).
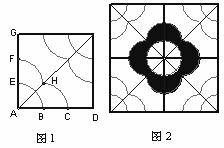
三、解答题(共5个小题,共25分)
13.(本小题满分5分)计算: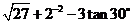 +
+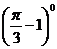 .
.
14.(本小题满分5分)解分式方程: .
.
15.(本小题满分5分)求不等式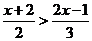 的正整数解.
的正整数解.
16.(本小题满分5分)已知2x-3=0,求代数式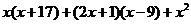 的值.
的值.
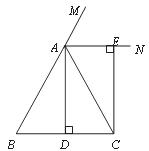
17.(本小题满分5分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
四、解答题(共2个小题,共10分)18.(本小题满分5分)
18.在梯形ABCD中,AD∥BC,AB=5,tanB=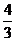 ,∠ACB=45
,∠ACB=45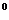 ,AD=2,求DC的长.
,AD=2,求DC的长.
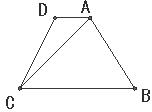
19.(本小题满分5分)已知:如图,AB是⊙O的直径,点C是⊙O上的一点,CD交AB的延长线于D,∠DCB=∠CAB.
(1) 求证:CD为⊙O的切线.
(2) 若CD=4,BD=2,求⊙O的半径长.
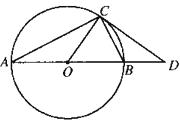
五、解答题(本题满分6分)20.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题: (1)求该班共有多少名学生?
(2)在图(1)中,将表示“步行”的部分补充完整.
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数.
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数.
六、解答题(共2个小题,共9分)
21.(本小题满分5分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?【利润=销售量×(销售单价-进价)】
22.(本小题满分4分)在平面直角坐标系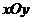 中,一次函数
中,一次函数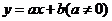 的图象l与
的图象l与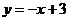 的图象关于y轴对称,直线l又与反比例函数
的图象关于y轴对称,直线l又与反比例函数 交于点
交于点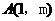 ,求m及k的值.
,求m及k的值.
七、解答题(本题满分7分)
23.四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
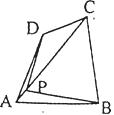
图1
八、解答题(本题满分7分)
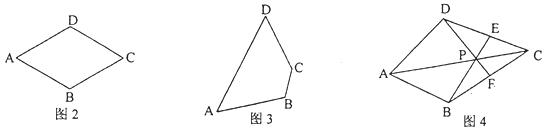
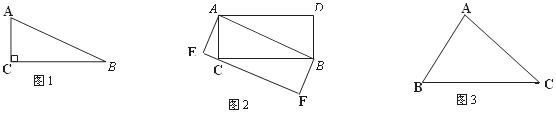
24.如图1中的△ABC是直角三角形,∠C=90º.现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合条件的矩形可以画出两个,如图2所示.
(1)设图2中的矩形ACBD和矩形AEFB的面积分别为S1和S2,则S1
S2(填“>”,“=”或“< ;(2)如图3中的△ABC是锐角三角形,且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 个,并在图3中把符合要求的矩形画出来.(3)在图3中所画出的矩形中,它们的面积之间具有怎样的关系?并说明你的理由;(4)猜想图3中所画的矩形的周长之间的大小关系,不必证明.
;(2)如图3中的△ABC是锐角三角形,且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 个,并在图3中把符合要求的矩形画出来.(3)在图3中所画出的矩形中,它们的面积之间具有怎样的关系?并说明你的理由;(4)猜想图3中所画的矩形的周长之间的大小关系,不必证明.
九、解答题(本题满分8分)
25.如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数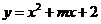 的图象经过点A、B,顶点为D.
的图象经过点A、B,顶点为D.
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转900后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com