
2008年天门市中考
数学试卷
第Ⅰ卷(选择题 共36分)
一.选择题(本大题共有12个小题,每小题3分,共36分)
1.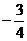 的倒数是( ).
的倒数是( ).
A、 B、
B、 C、
C、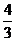 D、
D、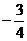
2.一个几何体的三视图如图所示,则这个几何体是( ).

3.关于x的一元二次方程(m-1)x2+x+m2-1=0有一根为0,则m的值为( ).
A、1
B、-
4.初三(1)班10名同学体育测试成绩如下表,那么这10名同学体育测试成绩的众数和中位数分别是( ).

A、38,36
B、38,
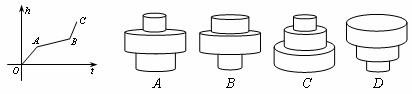
5.均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是图中( ).
6.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是( ).

A、75° B、65° C、55° D、50°
7.下列命题中,真命题是( ).
A、一组对边平行且有一组邻边相等的四边形是平行四边形
B、顺次连结四边形各边中点所得到的四边形是矩形
C、等边三角形既是轴对称图形又是中心对称图形
D、对角线互相垂直平分的四边形是菱形
8.如图,为了测量河两案A、B两点的距离,在与AB垂直的方向点C处测得AC=a,
∠ACB=α,那么AB等于( ).

A、a?sinα B、a?tanα
C、a?cosα D、
9.将分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上,放在桌面上,随机抽取一张(不放回),接着再随机抽取一张,恰好两张卡片上的数字相邻的概率为( ).
A、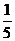 B、
B、 C、
C、 D、
D、
10.设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=
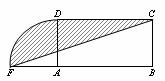
A、(4π+8)cm2 B、(4π+16)cm
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②

A、4个 B、3个 C、2个 D、1个
12.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则B’点的坐标为( ).

A、(2, )
B、(
)
B、( ,
, )
C、(2,
)
C、(2,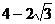 )
D、(
)
D、( ,
,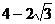 )
)
第Ⅱ卷(非选择题 共84分)
二.填空题(本大题有4个小题,每小题4分,共16分)
13.已知不等式组 的解集为-1<x<2,则(m+n)2008=_______________.
的解集为-1<x<2,则(m+n)2008=_______________.
14.如图,已知AE=CF,∠A=∠C,要使△ADF≌△CBE,还需添加一个条件___________
___________(只需写一个).

15.某公园门票价格如下表,有27名中学生游公园,则最少应付费______________元.(游客只能在公园售票处购票)
购票张数
1~29张
30~60张
60张以上
每张票的价格
10元
8元
6元
 16.如图是由火柴棒搭成的几何图案,则第n个图案中有__________________根火柴棒.(用含n的代数式表示)
16.如图是由火柴棒搭成的几何图案,则第n个图案中有__________________根火柴棒.(用含n的代数式表示)

三.解答题(本大题共有8个小题,共68分)
17.(本小题满分6分)计算:
18.(本小题满分7分)先化简,后求值: ?
?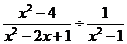 ,其中x2-x=0.
,其中x2-x=0.
19.(本小题满分7分)如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,2,3这三个数字;转盘B被均匀地分成4等分,每份分别标有4,5,6,7这四个数字.有人为小明,小飞设计了一个游戏,其规则如下:①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明胜,否则小飞胜.

(1)请你用列表或树形图求出小明胜和小飞胜的概率;
(2)游戏公平吗?若不公平,请你设计一个公平的规则.
20.(本小题满分7分)现将四个全等的直角梯形透明纸片,分别放在方格纸中,方格纸的每个小正方形的边长均为1,并且直角梯形的每个顶点与小正方形的顶点重合.请你仿照例①,按如下要求拼图.
要求:①用四个全等的直角梯形,按实际大小拼成符合要求的几何图形;
②拼成的几何图形互不重叠,且不留空隙;
③拼成的几何图形的各顶点必须与小正方形的顶点重合.

21.(本小题满分8分)如图,直线y=x+1与双曲线 交于A、B两点,其中A点在第一象限.C为x轴正半轴上一点,且S△ABC=3.
交于A、B两点,其中A点在第一象限.C为x轴正半轴上一点,且S△ABC=3.
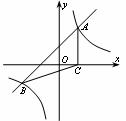
(1)求A、B、C三点的坐标;
(2)在坐标平面内,是否存在点P,使以A、B、C、P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
22.(本小题满分10分)如图,AB为⊙O的直径,C为⊙O上一点,∠BAC的平分线交⊙O于点D,过D点作EF∥BC交AB的延长线于点E,交AC的延长线于点F.

(1)求证:EF为⊙O的切线;
(2)若sin∠ABC= ,CF=1,求⊙O的半径及EF的长.
,CF=1,求⊙O的半径及EF的长.
23.(本小题满分11分)一快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日净收入.(日净收入=每天的销售额-套餐成本-每天固定支出)
(1)求y与x的函数关系式;
(2)若每份套餐售价不超过10元,要使该店日净收入不少于800元,那么每份售价最少不低于多少元?
(3)该店既要吸引顾客,使每天销售量较大,又要有较高的日净收入.按此要求,每份套餐的售价应定为多少元?此时日净收入为多少?
24.(本小题满分12分)如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为
(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒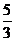 个单位长度的速度向终点B运动.设运动了x秒.
个单位长度的速度向终点B运动.设运动了x秒.

(1)点N的坐标为(________________,________________);(用含x的代数式表示)
(2)当x为何值时,△AMN为等腰三角形?
(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com