
2008年启东中学中考模拟考试
数学试卷(十四)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)
1.要使二次根式 有意义,
有意义,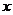 应满足的条件是
应满足的条件是
A.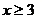 B.
B.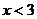 C.
C. D.
D.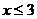
2.规定一种新的运算“*”:对于任意实数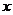 ,
,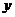 ,满足
,满足 。如
。如 ,则
,则
A.4 B.3 C.2 D.1
3.三峡工程是世界防洪效益最为显著的水利工程,它能有效控制长江上游洪水,增强长江中下游抗洪能力,据相关报道三峡水库的防洪库容为
A. B.
B.
C. D.
D.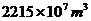
4.足球场平面示意图如图1所示,它是轴对称图形,其对称轴条数为

A.1条 B.2条
C.3条 D.4条
5.下列计算正确的是
A.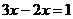 B.
B.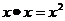
C.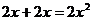 D.
D.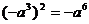
6.图

A.P区域 B.Q区域
C.M区域 D.N区域
7.正比例函数与反比例函数的图像都经过点(1,4),在第一象限内正比例函数的图像在反比例函数的图像上方,那么自变量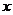 的取值范围是
的取值范围是
A. B.
B.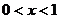 C.
C. D.
D.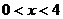
8.锐角三角形的三个内角是 ,
,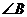 ,
, .如果
.如果 ,
, ,
,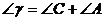 ,那么
,那么 ,
, ,
, 这三个角中
这三个角中
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
9.图3表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置
上小立方块的个数,则该几何体的主视图为

10.已知:如图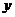 (cm2)关于运动时间
(cm2)关于运动时间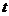 (s)的函数图像如图4b,若AB=
(s)的函数图像如图4b,若AB=

A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(共118分)
二、填空题(本大题共8小题,每小题3分,共24分,把答案填写在题中的横线上.)
11.在函数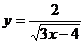 中,自变量
中,自变量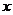 的取值范围是 .
的取值范围是 .
12.方程 的解是 .
的解是 .
13.如图5是某只股票从星期一至星期五每天的最高股价与最低股价的折线统计图,则这五天中最高股价与最低股价之差最大的一天是星期 .

14.如图6,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于 .

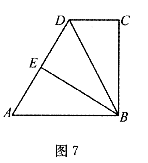
15.如图7,在梯形ABCD中, .AB∥CD,
.AB∥CD, .
. .将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为 .
.将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为 .
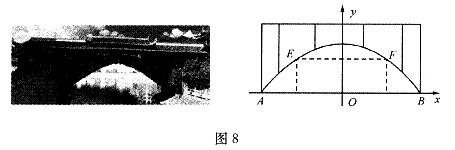
16.廊桥是我国古老的文化遗产.如图8,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为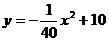 ,为保护廊桥的安全,在该抛物线上距水面AB高为
,为保护廊桥的安全,在该抛物线上距水面AB高为
17.如图9,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果 ,
, ,
, ,
, ,则
,则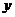 与
与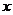 的关系是 .
的关系是 .
18.如图10,在由24个边长都为1的小正三角形的网格中,点P是正六边形的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长 。

三、解答题(本大题共10小题,满分94分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(本小题满分6分)计算或化简:
(1)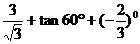
(2)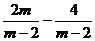
20.(本小题满分9分)亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图11,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C、D.然后测出两人之间的距离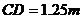 ,颖颖与楼之间的距离
,颖颖与楼之间的距离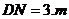 (C、D、N在一条直线上),颖颖的身高
(C、D、N在一条直线上),颖颖的身高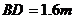 ,亮亮蹲在地上观测时眼睛到地面的距离
,亮亮蹲在地上观测时眼睛到地面的距离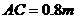 。你能根据以上测量数据帮助他们求出住宅楼的高度吗?
。你能根据以上测量数据帮助他们求出住宅楼的高度吗?
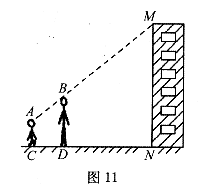
21.(本小题满分8分)姚明是我国著名的篮球运动员,他在这个赛季NBA常规赛中表现非常优异.下面是他在本赛季中,分别与“超音速”队和“快船”队各四场比赛中的技术统计.
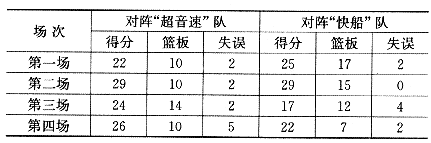
(1)请分别计算姚明在对阵“超音速”和“快船”两队的各四场比赛中,平均每场得多少分?
(2)请你从得分的角度分析,姚明在与“超音速”队和“快船”队的比赛中,对阵哪一个队的发挥更稳定?
(3)如果规定“综合得分”=平均每场得分×1+平均每场篮板× 1.5+平均每场失误×(一1.5),且综合得分越高表现越好,那么请你利用这种评价方法,来比较姚明在分别与“超音速”队和“快船”队的四场比赛中,对阵哪一个队表现得更好?
22.(本题8分)某校团委准备举办学生绘画展览,为美化画面,在长为

23.(本题8分)小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整:

方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解
解方程:
解:
方法二:利用二次函数图像与坐标轴的交点求解如图13所示,把方程 的解看成是二次函数
的解看成是二次函数 的图像与
的图像与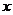 轴交点的横坐标,即
轴交点的横坐标,即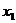 ,
, 就是方程的解.
就是方程的解.

方法三:利用两个函数图像的交点求解
(1)把方程 的解看成是一个二次函数
的解看成是一个二次函数 的图像与一个一次函数
的图像与一个一次函数 图像交点的横坐标;
图像交点的横坐标;
(2)画出这两个函数的图像,用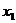 ,
, 在
在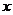 轴上标出方程的解.
轴上标出方程的解.
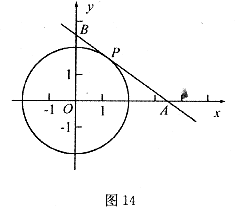
24.(本题满分10分)如图14,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与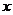 轴相交于点A,与
轴相交于点A,与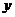 轴相交于点B.
轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由.
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
25.(本题10分)在课外活动时间,小王、小丽、小华做“互相踢踺子”游戏,踺子从一人传到另一人就记为踢一次.
(1)若从小丽开始,经过两次踢踺后,踺子踢到小华处的概率是多少?(用树状图或列表法说明)
(2)若经过三次踢踺后,踺子踢到小王处的可能性最小,应确定从谁开始踢,并说明理由.

26.(本题l2分)某校九年级三班为开展“迎2008年北京奥运会”的主题班会活动,派了小林和小明两位同学去学校附近的超市购买钢笔作为奖品.已知该超市的锦江牌钢笔每支8元,红梅牌钢笔每支4.8元,他们要购买这两种笔共40支.
(1)如果他们两人一共带了240元,全部用于购买奖品,那么能买这两种笔各多少支?
(2)小林和小明根据主题班会活动的设奖情况,决定所购买的锦江牌钢笔的数量要少于红梅牌钢笔的数量的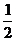 ,但又不少于红梅牌钢笔的数量的
,但又不少于红梅牌钢笔的数量的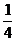 .如果他们买了锦江牌钢笔
.如果他们买了锦江牌钢笔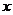 支,买这两种笔共花了
支,买这两种笔共花了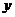 元.
元.
①请写出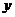 (元)关于
(元)关于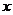 (支)的函数关系式,并求出自变量
(支)的函数关系式,并求出自变量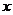 的取值范围.
的取值范围.
②请帮他们计算一下,这两种笔各购买多少支时,所花的钱最少,此时花了多少元?
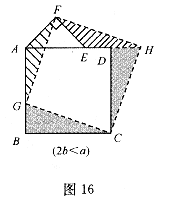
27.(本题10分)在图16~20中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边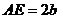 ,且边AD和AE在同一直线上.
,且边AD和AE在同一直线上.
操作示例:当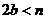 时,如图16,在BA上选取点G,使
时,如图16,在BA上选取点G,使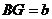 ,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90º到△FEH的位置,易知EH与AD在同一直线上.连接CH,由剪拼方法可得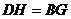 ,故△CHD
≌△CGB,从而又可将△CGB绕点C顺时针旋转90º到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图16),过点F作FM上AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,
,故△CHD
≌△CGB,从而又可将△CGB绕点C顺时针旋转90º到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图16),过点F作FM上AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,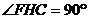 .进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究:
(1)正方形FGCH的面积是 ;(用含a,b的式子表示)
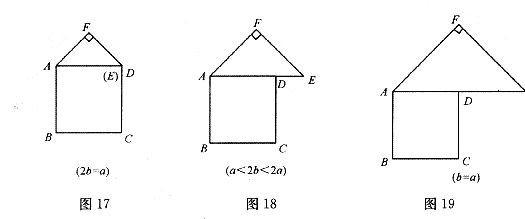
(2)类比图16的剪拼方法,请你就图17一图19的三种情形分别画出剪拼成一个新正方形的示意图.
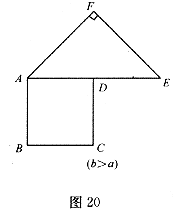
联想拓展:小明通过探究后发现:当 时,此类图形者能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移.当
时,此类图形者能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移.当 时,如图20的图形能否剪拼成一个正方形?若能请你在图中画出剪拼的示意图;若不能,简要说明理由.
时,如图20的图形能否剪拼成一个正方形?若能请你在图中画出剪拼的示意图;若不能,简要说明理由.
28.(本题13分)如图21,在平面直角坐标系中,已知点A(0, ),点B在z正半轴上,且
),点B在z正半轴上,且 .动点P在线段AB上从点A向点8以每秒
.动点P在线段AB上从点A向点8以每秒 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为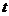 秒.在z轴上取两点M, N作等边△PMN.
秒.在z轴上取两点M, N作等边△PMN.
(1)求直线AB的解析式.
(2)求等边△PMN的边长(用t的代数式表示),并求出当等边△PMN的顶点M运动到与原点。重合时t的值.
(3)如果取OB的中点D,以0D为边在Rt△A()B内部作如图22所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当 秒时S与
秒时S与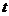 的函数关系式,并求出S的最大值。
的函数关系式,并求出S的最大值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com