
2008年启东中学中考模拟考试(十二)
数学试卷
本试卷分第I卷(选择题)和第Ⅱ卷两部分
第I卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)
1.4的算术平方根为
A.2 B.-
2.下列计算正确的是
A.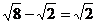 B.
B.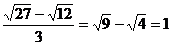
C.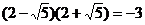 D.
D.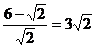
3.英寸是电视机常用规格之一,1英寸约为拇指上面一节的长,如图1所示,则7英寸长相当于

A.课本的宽度 B.课桌的宽度
C.黑板的高度 D.粉笔的长度
4.解分式方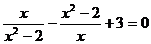 时,设
时,设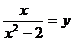 ,则原方程变形为
,则原方程变形为
A.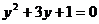 B.
B.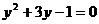
C.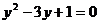 D.
D.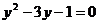
5.小颖从家出发,直走了20min,到一个离家
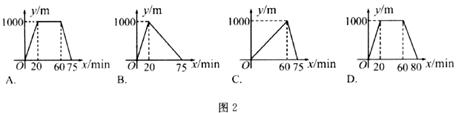
6.如图3所示,路灯距地面
A.增大
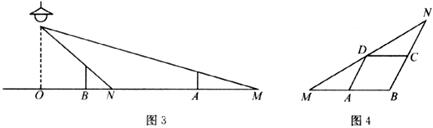
7.如图4所示,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,则□ABCD的周长是
A.24 B.
8.小敏在某次投篮中,球的运动线路是抛物线 的一部分,如图5所示,若命中篮圈中心,则他与篮底的距离
的一部分,如图5所示,若命中篮圈中心,则他与篮底的距离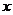 是
是
A.
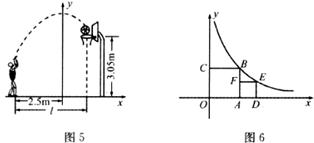
9.如图6所示,正方形OABC、ADEF的顶点A、D、C在坐标轴上,点F在AB上,点B、E在函数 的图像上,则点E的坐标是
的图像上,则点E的坐标是
A.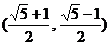 B.
B.
C.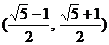 D.
D.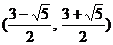
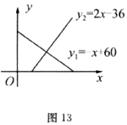
10.在平面直角坐标系中,已知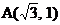 ,O(0,0),
,O(0,0), 三点,AE平分∠OAC,交OC于E,则直线AE对应的函数表达式是
三点,AE平分∠OAC,交OC于E,则直线AE对应的函数表达式是
A. B.
B.
C. D.
D.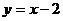
第Ⅱ卷(共118分)
二、填空题(本大题共8小题,每小题3分,共24分,把答案填写在题中的横线上。)
11.据媒体报道,今年“五一”黄金周期间,我市旅游收入再创历史新高,达1290000000元,用科学记数法表示为 元。
12.若方程生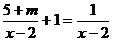 无解,则m=
。
无解,则m=
。
13.一次函数 的图像经过点
的图像经过点 和
和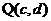 ,则
,则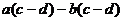 的值为
。
的值为
。
14.一组数据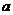 ,
, ,
, ,
,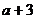 ,
, ,
,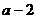 ,
, 的中位数是
。
的中位数是
。
15.学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为符合设计要求的图案是图7中的 (将所有符合设计要求的图案序号填上)。

16.如图8,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为 。

17.现为如图9所示是某种型号的正六角螺母毛坯的三视图,则它的表面积为 cm2。

18.如图10所示,将边长为1的正方形OAPB沿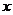 轴正方向连续翻转2007次,点P依次落在点P1,P2,P3,……,P2007的位置,则P2007得横坐标
轴正方向连续翻转2007次,点P依次落在点P1,P2,P3,……,P2007的位置,则P2007得横坐标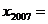 。
。
三、解答题(本大题共10小题,满分94分。解答应写出必要的文字说明、证明过程或推演步骤)
19.(本题满分5分)解不等式组:
20.(本题满分5分)
先化简,再求值: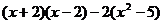 ,其中
,其中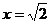 。
。
21.(本题满分7分)
图

(1)2000年,中国60岁及以上人口数为 亿,15~59岁人口数为 亿(精确到0.01亿).
(2)预计到2050年,中国总人口数将达到 亿,60岁及以上人口数占总人口数的 %(精确到0.01亿)。
(3)通过对中国人口发展情况统计图的分析,写出两条你认为正确的结论。
22.(本题10分)
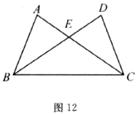
在一次数学活动中,黑板上画着如图12所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
①AB=DC ②∠ABE=∠DCE ③AE=DE ④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张。
请结合图形解答下列两个问题:
(1)当抽得①和②时,用①,②作为条件能判定△BEC是等腰三角形吗?说说你的理由。
(2)请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,使△EBC不能构成等腰三角形的概率。
23.(本小题满分12分)
某地区一种商品的需求量 (万件)、供应量
(万件)、供应量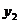 (万件)与价格
(万件)与价格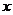 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: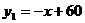 ,
, 。需求量为0时,即停止供应。当
。需求量为0时,即停止供应。当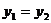 时,该商品的价格称为稳定价格,需求量称为稳定需求量。
时,该商品的价格称为稳定价格,需求量称为稳定需求量。
(1)求该商品的稳定价格与稳定需求量。
(2)价格在什么范围,该商品的需求量低于供应量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量。现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
24.(本小题满分9分)
某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图14所示,BC∥AD,斜坡AB长
(1)求改造前坡顶与地面的距离BE的长(精确到
(2)为确保安全,学校计划改造时保持坡脚A不动,坡顶B沿BC前进到F点处,问BF至少是多少米(精确到
(参考数据:sin68°=0.9272,cos68°=0.3746,tan68°=2.4751,sin50°=0.7660,
cos50°=0.6428,tan50°=1.1918)

25.(本小题满分10分)
你知道吗?一个足球被从地面向上踢出,它距地面高度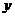 (m)可以用二次函数
(m)可以用二次函数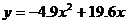 刻画,其中
刻画,其中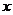 (s)表示足球被踢出后经过的时间。
(s)表示足球被踢出后经过的时间。
(1)方程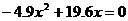 的根的实际意义是 。
的根的实际意义是 。
(2)求经过多长时间,足球到达它的最高点?最高点的高度是多少?
26.(本题10分)
根据以下10个乘积,回答问题:
11×29 12×28 13×27 14×26 15×25
16×24 17×23 18×22 19×21 20×20
(1)试将以上各乘积分别写成一个“□2-○
(2)若乘积的两个因数分别用字母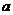 ,
,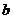 表示(
表示(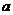 ,
,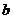 为正数),请观察给出面与
为正数),请观察给出面与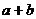 的关系式。(不要求证明)
的关系式。(不要求证明)
(3)若用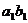 ,
, ,……,
,……,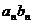 表示
表示 个乘积,其中
个乘积,其中 ,
,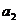 ,
,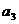 ,……
,…… ,
,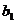 ,
, ,
, ,……
,……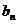 为正数。请根据(1)中乘积的大小顺序猜测出一个一般结论。(不要求证明)
为正数。请根据(1)中乘积的大小顺序猜测出一个一般结论。(不要求证明)
27.(本题12分)
如图15,半圆O为△ABC的外接半圆,AC为直径,D为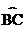 上的一动点。
上的一动点。
(1)问添加一个什么条件后,能使得 ?请说明理由。
?请说明理由。
(2)若AB∥OD,点D所在的位置应满足什么条件?请说明理由。
(3)如图16,在(1)和(2)的条件下,四边形AODB是什么特殊的四边形?证明你的结论。
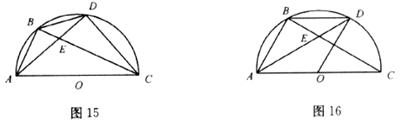
28.(本小题满分14分)
如图17,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,OA=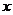 轴匀速向点C运动,到达点C即停止。设点P运动的时间为t s.
轴匀速向点C运动,到达点C即停止。设点P运动的时间为t s.
(1)过点P作对角线OB的垂线,垂足为点T。求PT的长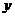 与时间t的函数关系式,并写出自变量t的取值范围。
与时间t的函数关系式,并写出自变量t的取值范围。
(2)在点P运动过程中,当点O关于直线AP的对称点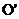 恰好落在对角线OB上时,求此时直线AP的函数解析式。
恰好落在对角线OB上时,求此时直线AP的函数解析式。
(3)探索:以A,P,T三点为顶点的△APT的面积能否达到矩形OABC 面积的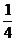 ?请说明理由。
?请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com