
2007-2008学年度枣庄市第二学期七年级期末检测
数学试卷
一、选择题:每小题4分,共40分.
1.下列运算正确的是
A.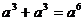
B.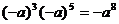
C.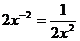
D.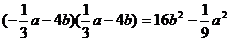
2.根据下列条件作三角形,不能唯一确定三角形的是
A.已知三个角 B.已知三条边
C.已知两角和夹边 D.已知两边和夹角
3.木工师傅想制作一个三角形的工具,他应该选用下列哪一组木条
A.25,48,80 B.15,47,62
C.32,60,68 D.25,59,30
4.如图,△ABC中,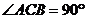 ,把△ABC沿AC翻折180º,使点B落在
,把△ABC沿AC翻折180º,使点B落在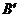 位置.在
位置.在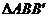 中,关于线段AC的性质,不正确的说法是
中,关于线段AC的性质,不正确的说法是
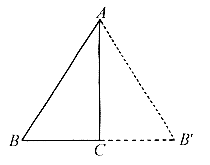
A.AC是边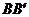 上的中线
上的中线
B.AC是边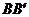 上的高
上的高
C.AC是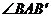 的角平分线
的角平分线
D.AC=2BC
5.下列图案中,轴对称图形是

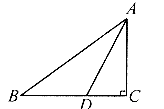
6.如图,在Rt△ABC中,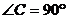 ,
, 的角平分线AD交BC于点D,CD=2,则点D到AB的距离是
的角平分线AD交BC于点D,CD=2,则点D到AB的距离是
A.1 B.2 C.3 D.4
7.若一个等腰三角形两内角的度数之比为1┱4,则这个等腰三角形顶角的度数为
A.20º B.120º C.20º或l20º D.36º
8.要测量河岸相对两点A,B的距离,先在AB的垂线BF上取两点c,D使CD=BC;再定出BF的垂线DE,使A,C,E在一条直线上(如图).可以说明△EDC△ABC,得ED=AB,因此测得ED之长即为AB的距离.判定△EDC≌△ABC的理由是
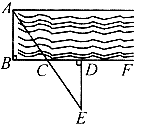
A.SAS B.ASA C.SSS D.HL
9.一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同.在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率为
A.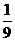 B.
B.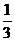 C.
C.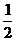 D.
D.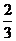
10.甲、乙两同学从/4地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时问t(时)之问的函数关系的图像如图所示.根据图中提供的信息,有下列说法:
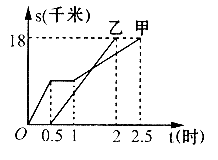
①他们都行驶了
②甲中途停留了0.5小时
③乙比甲晚出发0.5小时
④相遇后甲的速度小于乙的速度
⑤甲、乙两人同时到达目的地
其中,符合图象描述的说法有
A.2个 B.3个 C.4个 D.5个
二、填空题:每小题4分。共24分,把答案填在题中横线上.
11.2008年北京奥运会火炬接力,火炬手约为21780人,把这个数据用科学记数法表示约为 人(保留两个有效数字).
12.一个角的度数是40º,那么它的余角的补角的度数是 .
13.某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车牌号码如图所示,则该汽车的号码是 .
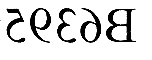
14.如图,三角形纸片ABC中,AB=
15.
输入数据
1
2
3
4
5
6
输出数据
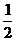
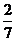
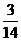
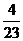
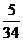
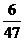
那么,当输入数据7时,输出的数据是
16.将4个实数a,b,c,d排成2行、2列,两边各加一条竖线记成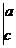
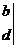 ,定义
,定义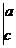
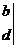
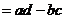 上述记号就叫做2阶行列式.若
上述记号就叫做2阶行列式.若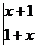
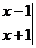
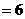 ,则
,则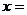 。
。
三、解答题:本大题共6小题。共56分.
17.计算:(每小题4分,满分8分)
(1)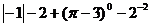 ;
;
(2)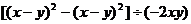
18.(本题满分8分)
如图,C,E分别在直线AB,DF上,小华想知道∠ACE和∠DEC是否互补,但他又没有带量角器,只带了一副三角板,于是他想了这样一个办法:连结CF,找出CF的中点O,然后连结EO并延长EO和直线AB相交于点曰,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上理由.
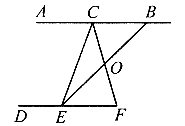
小华是这样想的:
因为CF和BE相交于点O,
根据 ,得∠COB=∠FOE.
而0是CF的中点,那么CO=FO.又已知EO=BO,
根据 ,得△COB≌△FOE.
所以BC=EF,∠BCO=∠F.
又∠BCO=∠F,根据 ,得AB∥DF.
根据 ,得∠ACE+∠DEC=180º.
19.(本题满分10分)
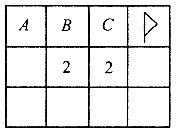
“扫雷”是一个有趣的游戏,上图是此游戏的一部分:
图中数字2表示以该数字为中心的8个方格中有2个地雷,小旗表示该方格已被探明有地雷,现在还剩下A,B,C三个方格未被探明,其它地方为安全区(包括有数字的方格).试问:
(1)现在还剩下几个地雷?
(2)A,B,C三个方格中有地雷的概率分别是多少?
20.(本题满分10分)
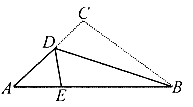
如图,已知AB=AC,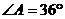 ,AB的垂直平分线MN交AC于点JD,交AB于点M.有
,AB的垂直平分线MN交AC于点JD,交AB于点M.有
下面3个结论:
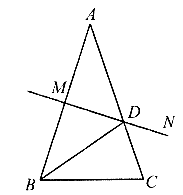
①射线BD是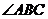 的角平分线;
的角平分线;
②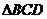 是等腰三角形;
是等腰三角形;
③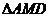 ≌
≌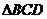 .
.
(1)正确的结论是哪几个?
(2)从你认为正确的结论中选一个说明理由
21.(本题满分l0分)
如图,阴影部分是由5个小正方形组成的一个直角图形.请用二种方法分别在下图方格内涂黑二个小正方形,使涂黑部分与阴影部分组成的图形成为轴对称图形
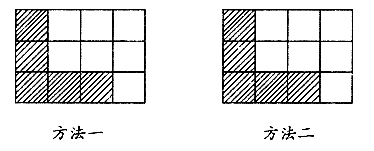
22.(本题满分l0分)
某公司决定投资新项目,通过考察有6个项目可供选择,各项目所需资金及预计年利润如下表:
所需资金/亿元
1
2
4
6
7
8
预计年利润/千万元
0.2
0.35
0.55
0.7
0.9
1
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果投资一个4亿元的项目,则其年利润预计有多少?
(3)如果预计获得0.9千万元年利润,投资一个项目需要多少资金?
(4)如果该公司拿出10亿元,可以进行哪些项目的投资?预计最大年利润是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com