
2007-2008学年度滨城区第二学期八年级期末学业水平测试
数学试卷
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,每小题3分,计30分。下列各小题所给出的四个答案选项中只有一个是正确的,请你选出来填在第Ⅱ卷上的第Ⅰ卷答案栏内,选对得3分,否则均得零分。
1.若分式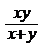 中的x、y的值都变为原来的3倍,则此分式的值( )
中的x、y的值都变为原来的3倍,则此分式的值( )
A.不变 B.是原来的3倍 C.是原来的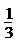 D.是原来的
D.是原来的 倍
倍
2.若关于x的分式方程 ―2=
―2=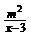 无解,则m的值是( )
无解,则m的值是( )
A. B.―
B.― C.
C.
 D.不确定
D.不确定
3.如图已知k>0,则函数y=kx与y=- 的图像大致是( )
的图像大致是( )

A.第一、二象限 B. 第三、四象限 C.第一、三象限 D.第二、四象限
4.已知一次函数y=kx+b的图像经过第一、二、四象限,则反比例函数y= 的图像在( )
的图像在( )
5.已知平行四边形的一条边长为4,下列各数不能作为它的两条对角线长的是( )
A.10与6 B.12与
6.若顺次连接四边形各边中点所得的四边形是菱形,则原四边形一定是( )
A.平行四边形 B. 矩形 C. 菱形 D.对角线相等的四边形
7.若等腰梯形的两底之差等于一腰长,则此梯形中的锐角为( )
A.30 度 B.45度 C.60度 D.75度
8.对于数据组2, 4, 4, 5, 3, 9, 4, 5, 1, 8, 其众数、中位数与平均数分别为( )
A. 4, 4, 6 B.4, 6,
9.已知样本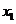 ,
, ,…
,…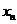 的方差是2, 则样本3
的方差是2, 则样本3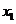 +5,3
+5,3 +5,…3
+5,…3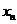 +5的方差是( )
+5的方差是( )
A.11
B.
10.2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则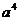 +
+ 的值为( )
的值为( )
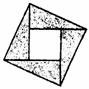
A. 35 B.
第Ⅱ卷(非选择题 共70分)
二、本大题共10个小题,每小题3分,计30分.只要求填写最简结果,不写中间推理演算过程
11.当x___________时,分式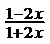 有意义.
有意义.
12.当x_________时,分式 的值为零.
的值为零.
13.甲、乙两人分别从相距目的地
14.有两棵树,一棵高
15.若函数y=(m+1)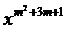 是反比例函数,则m的值为______________.
是反比例函数,则m的值为______________.
16.函数y=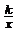 (k>0)的图象上有三点
(k>0)的图象上有三点 (
(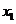 ,
, ),
), 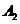 (
( ,
, ),
),  (
( ,
,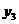 ),
),  (
(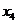 ,
, ).且
).且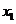 <
< < 0 <
< 0 < ,则
,则 ,
, ,
,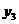 的大小为______________.
的大小为______________.
17.菱形有一个角是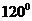 ,有一条对角线长6为,则菱形的边长为______________.
,有一条对角线长6为,则菱形的边长为______________.
18.在梯形ABCD中,AB∥CD, AB>CD, CE∥DA交AB于点E,并且△BCE的周长为
19.数据10001,10002,10003,10004,10005的样本方差是_____________________.
20.人数相等的甲乙两班的学生参加了同一次数学测验,甲班的平均分和方差分别为80和240,乙班的平均分和方差分别是80和180,则成绩较整齐的是_______班.
三、本大题共5个小题,计40分.解答要求写出文字说明或推理演算过程.
21.某汽车的功率p为一定值,汽车行驶时的速度v(米/秒)与它受的牵引力F(牛)之间的函数关系如图所示.
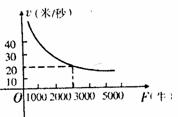
(1)这辆汽车的功率是多少?请写出这一函数的表达式.
(2)当它所受牵引力为1200牛时,汽车速度为多少千米/时?
22.(1)化简(x-1-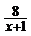 )÷
)÷ , 将x=3-
, 将x=3-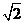 代入求值.
代入求值.
(2)解分式方程:  +1=
+1=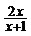
23.为了考查甲、乙两种小麦的长势,分别从中抽取10株麦苗,测得苗高如下(单位: cm)
甲 12, 13, 14, 15, 10, 16, 13, 11, 15, 11
乙 11, 16, 17, 14, 13, 19, 6, 8, 10, 16
(1)分别计算两种小麦的平均苗高;
(2)哪种小麦的长势比较整齐?
24.如图,一次函数y=kx+b的图象与反比例函数y= 图象交于A(-2,1)、B(1,n)两点.
图象交于A(-2,1)、B(1,n)两点.

(1) 求反比例函数和一次函数的解析式.
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
25.如图所示△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1) 求证: EO=FO.
(2)点O运动到何处时,四边形AECF是矩形?并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com