
2008年滕州市九年级质量检测数学试卷
第Ⅰ卷(选择题共36分)
一、选择题:(本大题共l2小题,每小题3分。共36分.在每小题给出的四个选项中。只有一个选项符合题目要求。将代号填入卷Ⅱ表格内.)
1.我市某天的最高气温为
A.
2.在平面直角坐标系中,点P(一3,4)到 轴的距离为
轴的距离为
A.3 B.一3 C .4 D.一4
3.如图(1),在平行四边形ABCD中,CE AB,E为垂足,如果
AB,E为垂足,如果 A=125º,则
A=125º,则 BCE=
BCE=

图(1)
A.550 B.
4.下列各式中正确的是
A.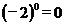 B.
B.
C. D.
D.
5.如图(2),数轴上一动点A向左移动2个单位长度到达点B再向右移动5个单位长度到达点C,若点C表示的数为l,则点A表示的数为
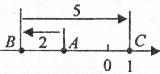
图(2)
A.7 B.
6.图(3)为一个多面体的表面展开图,每个面内都标注了数字.若数字为3的面是底面,则朝上一面所标注的数字为
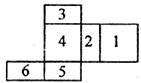
图(3)
A.2 B.
7.某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工l6吨.现计划用l5天完成加工任务,该公司应安排几天精加工,几天粗加工?设安排 天精加工,
天精加工,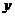 天粗加工.为解决这个问题,所列方程组正确的是
天粗加工.为解决这个问题,所列方程组正确的是
A.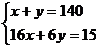 B.
B.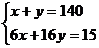
C. D.
D.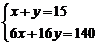
8.某射击小组有20人,教练根据他们某次射击的数据绘制成如图(4)所示的统计图,则这组数据的众数和中位数分别是

图(4)
A.7,7 B.8,7.
9.某商贩去菜摊买黄瓜,他上午买了30斤,价格为每斤 元;下午,他又买了20斤,价格为每斤
元;下午,他又买了20斤,价格为每斤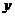 元.后来他以每斤
元.后来他以每斤 元的价格卖完后,结果发现自己赔了钱,其原因是
元的价格卖完后,结果发现自己赔了钱,其原因是
A. <
<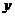 B.
B. >
>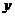 C.
C. ≤
≤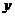 D.
D.
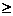
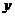
10.如图(5),把矩形纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若 FPH=90º,PF=8,PH=6,则矩形ABCD的边BC长为
FPH=90º,PF=8,PH=6,则矩形ABCD的边BC长为

图(5)
A.20 B.
11.已知一次函数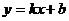 的图象如图(6)所示,当
的图象如图(6)所示,当 <1时,
<1时,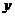 的取值范围是
的取值范围是
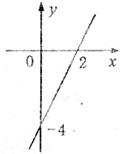
图(6)
A.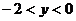 B.
B.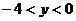
C.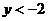 D.
D.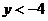
12.如图(7),MN是⊙O的直径,MN=2,点A在⊙O 上, ,B为弧
,B为弧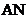 的中点,P是直径MN上一动点,则PA十PB的最小值为
的中点,P是直径MN上一动点,则PA十PB的最小值为
图(7)
A.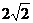 B.
B.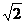 C.1 D.2
C.1 D.2
第Ⅱ卷(非选择题共84分)
二、填空题:本大题共6小题,每小题3分,共l8分.把答案填在题中的横线上.
13.4的算术平方根是 .
14.分解因式: .
.
15.已知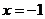 是关于
是关于 的方程
的方程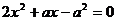 的一个根,则a=
.
的一个根,则a=
.
16.用图(8)所示的正方形和长方形卡片若干张,拼成一个长为

图(8)
17.刘强同学为了调查全市初中生人数,他对自己所在城区人El和城区初中生人数作了调查:城区人口约3万,初中生人数约l200.全市人口实际约300万,为此他推断全市初中生人数为l2万.但市教育局提供的全市初中生人数约8万,与估计数据有很大偏差.请你用所学的统计知识,找出其中错误的原因 .
18.如图(9),半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于 .

图(9)
三.本大题共9小题,满分66分。解答应写出文字说明、说理过程或演算步骤。
19.计算: .(本小题满分6分)
.(本小题满分6分)
20.当 时,求
时,求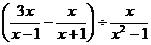 的值.(本小题满分6分)
的值.(本小题满分6分)
21.解不等式组 ①②,并将解集在数轴上表示出来。(本小题满分6分)
①②,并将解集在数轴上表示出来。(本小题满分6分)
22.已知⊙O1经过A(一4,2),B(一3,3),C(一1,一l),O(0,0)四点,一次函数 的图象是直线l,直线l与
的图象是直线l,直线l与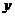 轴交于点D.
轴交于点D.
(1)在下面的平面直角坐标系中画出⊙O1,直线l与⊙O1的交点坐标为 ;
(2)若⊙O1上存在整点P(横坐标与纵坐标均为整数的点称为整点),使得△APD为等腰三角形,所有满足条件的P坐标为 ;
(3)将⊙O1沿 轴向右平移
个单位时,⊙O1与
轴向右平移
个单位时,⊙O1与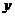 抽相切。
抽相切。
23.已知,如图(10),延长 ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到
ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到 DEF为等边三角形.(本小题满分6分)
DEF为等边三角形.(本小题满分6分)
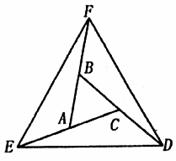
图(10)
求证:(1)△AEF △CDE;
△CDE;
(2) △ABC为等边三角形.
24.如图(11),反比例函数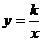 的图象与一次函数
的图象与一次函数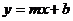 的图象交于A(1,3),B(n,一l)两点.(本小题满分8分)
的图象交于A(1,3),B(n,一l)两点.(本小题满分8分)
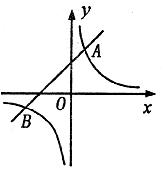
图(11)
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
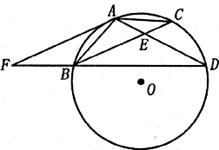
25.如图(12),点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=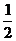 ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=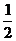 BD,连接AF.(本小题满分9分)
BD,连接AF.(本小题满分9分)
图(12)
(1)求证:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
26.如图(13),小山上有一棵树.现有测角仪和皮尺两种测量工具,请你设计一种测量方案,在山脚水平地面上测出小树顶端A到水平地面的距离AB.要求:(本小题满分9分)

图(13)
(1)画出测量示意图;
(2)写出测量步骤(测量数据用字母表示);
(3)根据(2)中的数据计算树高AB.
27.如图(14),抛物线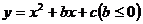 的图象与
的图象与 轴交于A,B两点,与
轴交于A,B两点,与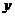 轴交于点C,其中点A的坐标为(-2,0).直线
轴交于点C,其中点A的坐标为(-2,0).直线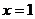 与抛物线交于点E,与
与抛物线交于点E,与 轴交于点F,且
轴交于点F,且 .(本小题满分10分)
.(本小题满分10分)
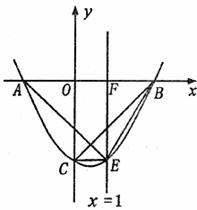
图(14)
(1)用b表示点E的坐标;
(2)求实数b的取值范围;
(3)请问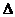 BCE的面积是否有最大值?若有,求出这个最大值;若没有,请说明理由.
BCE的面积是否有最大值?若有,求出这个最大值;若没有,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com