
2007-2008学年度潍坊市高密第二学期八年级期末考试
数学试卷
(时间90分钟 满分120分)
一、选择题(共10个小题,每小题3分,共30分)
1.计算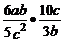 的结果是( )
的结果是( )
(A)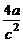 (B)
(B)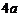 (C)
(C)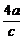 (D)
(D)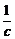
2.如图,小手盖住的点的坐标可能为( ).
(A)(5,2) (B)(―6,3) (C)( ―4,―6) (D)(3,―4)

3.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出四边形ABCD是正方形,那么这个条件是( )
(A)∠D=90° (B)AB=CD (C)AD=BC (D)BC=CD
4.下列判断中错误的是( )
(A)有两角和一边对应相等的两个三角形全等
(B)有两边和一角对应相等的两个三角形全等
(C)有两边和其中一边上的中线对应相等的两个三角形全等
(D)有一边对应相等的两个等边三角形全等
5.下列命题中,真命题是( )
(A)两条对角线垂直的四边形是菱形
(B)对角线垂直且相等的四边形是正方形
(C)两条对角线相等的四边形是矩形
(D)两条对角线相等的平行四边形是矩形
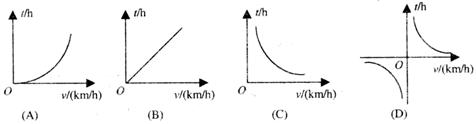
6.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)与行驶速度v(km/h)的函数关系图象大致是( )
7.一次函数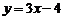 的图象不经过( )
的图象不经过( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
8.甲、乙、丙二名射击运动员在某场测试中各射击20次,3人的测试成绩如下表
甲的成绩
环数
7
8
9
10
频数
4
6
6
4
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
5
5
5
5
则甲、乙.丙3名运动员测试成绩最稳定的是( )
(A)甲 (B)乙 (C)丙 (D)3人成绩稳定情况相同
9.为了了解某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨)
4
5
6
9
户数
3
4
2
1
则关于这10户家庭的月用水量,下列说法错误的是( )
(A)中位数是5吨 (B)极差是3吨
(C)平均数是5.3吨 (D)众数是5吨
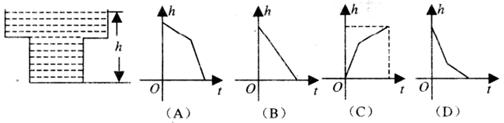
10.某蓄水池横断面示意图如图,分深水区和浅水区;如果这个注满水的蓄水池以周定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )
二、填空题(共8个小题,每个小题3分,共24分)
11.若点M(1,
12.任意一个平行四边形,当它的一个锐角增大到_________度时,就变成了矩形;当它的一组邻边变到____________时,就变成了菱形;当它的对角线变到__________时,就变成了正方形.
13.函数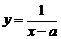 ,当
,当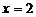 时没有意义,则
时没有意义,则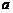 的值为_________.
的值为_________.
14.某函数的图象经过点(1,―10),且函数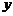 的值随自变量
的值随自变量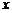 的增大而增大,请写出一个符合上述条件的函数关系式:__________________.
的增大而增大,请写出一个符合上述条件的函数关系式:__________________.
15.随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量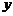 (g/m3)与大气压强
(g/m3)与大气压强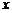 (kpa)成正比例函数关系.当
(kpa)成正比例函数关系.当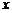 =36(kpa)时,
=36(kpa)时,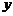 =108(g/m3),请写出
=108(g/m3),请写出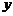 与
与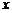 的函数关系式:__________________.
的函数关系式:__________________.
16.如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线(请保留画图痕迹).

17.请选择一组a、b的值,写出一个关于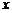 为未知数且形如
为未知数且形如 的分式方程,使它的解是
的分式方程,使它的解是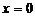 ,这样的分式方程可以是_________.
,这样的分式方程可以是_________.
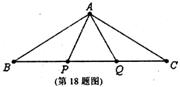
18.如图,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于_________.
三、解答题(共8个小题,满分66分)
19.(本题满分7分)
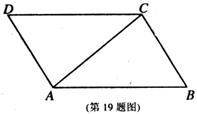
如图,AC是平行四边形ABCD的对角线.
(1)请按如下步骤在图中完成作图(保留作图痕迹):
①分别以A,C为圆心,以大于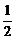 AC长为半径画弧,弧在AC两侧的交点分别为P,Q;
AC长为半径画弧,弧在AC两侧的交点分别为P,Q;
②连结PQ,PQ分别与AB,AC,CD交于点E,O,F.
(2)求证:AE=CF.
20.(本题满分8分)
2008年初我国南方发生雪灾,某地电线被雪压断,供电局的维修队要到30千米远的郊区进行抢修.维修工骑摩托车先走,15分钟后,抢修车装载所需材料出发,结果两车同时到达抢修点。已知抢修车的速度是摩托车速度的1.5倍,求两种车的速度.
21.(本题满分8分)小青在八年级上学期的数学成绩如下表所示
测验类别
平时
期中考试
期末考试
测验1
测验2
测验3
测验4
成绩
88
70
98
86
90
87
(1)计算小青该学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,请计算出小青该学期的总评成绩。

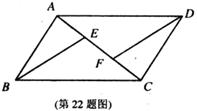
22.(本题满分8分)如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
猜想:
证明:
23.(本题满分7分)在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后.把相关知识归纳整理如下:
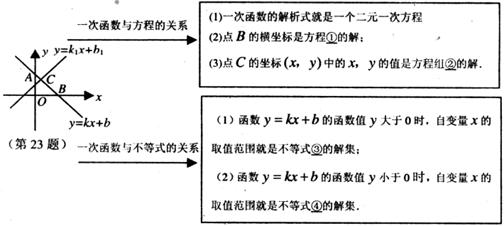
(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
①___________________________;②___________________________;
③___________________________;④___________________________;
(2)如果点C的坐标为(1,3),那么不等式 的解集是__________________.
的解集是__________________.
24.(本题满分9分)解答一个问题后,将结论作为条件之一,提出原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设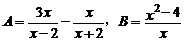 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
25.(本题满分10分)如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.

(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足__________________条件时,四边形DAEF是矩形;
②当△ABC满足__________________条件时,四边形DAEF是菱形;
③当△ABC满足__________________条件时,以D、A、E、F为顶点的四边形不存在.
26.(本题满分10分)
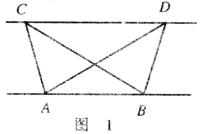
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
①如图2,点M,N在反比例函数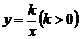 的图象上,过点M作ME⊥
的图象上,过点M作ME⊥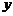 轴,过点N作NF⊥
轴,过点N作NF⊥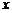 轴,垂足分别为F,F.
轴,垂足分别为F,F.
试证明:MN∥EF.
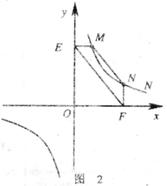
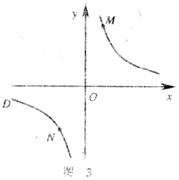
②若①中的其他条件不变,只改变点M,N的付置如图3所示,请判断MN与EF是否平行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com