
2008年广东省初中毕业生学业考试
数学试卷
一、选择题(本大题5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一项是符合题目要求的。
1.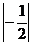 的值是
的值是
A.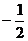 B.
B.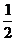 C.-2 D.2
C.-2 D.2
2.
A.408.2×
C.4.082×
3.下列式子中是完全平方式的是
A. B.
B.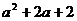 C.
C. D.
D.
4.下列图形中是轴对称图形的是

5.下表是我国部分城市气象台对五月某一天最高温度的预报,当天预报最高温度数据的中位数是
城市
北京
上海
杭州
苏州
武汉
重庆
广州
汕头
珠海
深圳
最高温度(℃)
26
25
29
29
31
32
28
27
28
29
A.28 B.
二、填空题(本大题5小题,每小题4分,共20分)
6.-2的相反数是 。
7.经过点A(1,2)的反比例函数解析式是 。
8.已知等边三角形ABC的边长为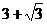 ,则△ABC的周长是 。
,则△ABC的周长是 。
9.如下图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=120°,则∠ANM= 。

10.如下图,已知AB是⊙O的直径,BC为弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连结DC,则∠DCB= 。

三、解答题(一)(本大题5小题,每小题6分,共30分)
11.(本题满分6分)
计算: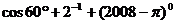
12.(本题满分6分)
解不等式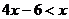 ,并将不等式的解集表示在数轴上。
,并将不等式的解集表示在数轴上。
13.(本题满分6分)
如下图,在△ABC中,AB=AC=10,BC=8。用尺规作图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长。

14.(本题满分6分)
已知直线 :
: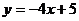 和直线
和直线 :
: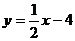 ,求两条直线
,求两条直线 和
和 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上。
的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上。
15.(本题满分6分)
如下图,在长为

四、解答题(二)(本大题4小题,每小题7分,共28分)
16.(本题满分7分)
在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电,该地供电局组织电工进行抢修。供电局距离抢修工地
17.(本题满分7分)
一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其他都相同),其中有白球2个,黄球1个。若从中任意摸出一个球,这个球是白球的概率为0.5。
(1)求口袋中红球的个数。
(2)小明认为口袋中共有三种颜色的球,所以从口袋中任意摸出一球,摸到红球、白球或黄球的概率都是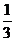 ,你认为对吗?请你用列表或画树状图的方法说明理由。
,你认为对吗?请你用列表或画树状图的方法说明理由。
18.(本题满分7分)
如下图,在△ABC中,BC >AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF。
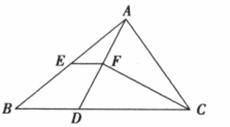
(1)求证:EF∥BC。
(2)若四边形BDFE的面积为6,求△ABD的面积。
19.(本题满分7分)
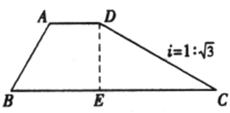
如下图,梯形ABCD是拦水坝的横断面图,(图中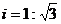 是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积。(结果保留三位有效数字。参考数据:
是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积。(结果保留三位有效数字。参考数据: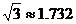 ,
,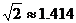 )
)
五、解答题(三)(本大题3小题,每小题9分,共27分)
20.(本题满分9分)
(1)解方程求出两个解 、
、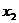 ,并计算两个解的和与积,填入下表
,并计算两个解的和与积,填入下表
方程

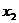
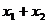

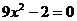

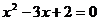
关于 的方程
的方程 (
( 、
、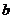 、
、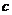 为常数,且
为常数,且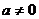 ,
, )
)
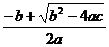

(2)观察表格中方程两个解的和、两个解的积与原方程系数之间的关系有什么规律?写出你的结论。
21.(本题满分9分)
(1)如图甲,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC。求∠AEB的大小。
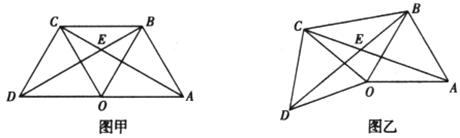
(2)如图乙,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和△OCD不能重叠)。求∠AEB的大小。
22.(本题满分9分)
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD。
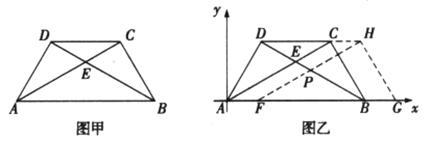
(1)填空:如图甲,AC= ,BD= ;四边形ABCD是 梯形。
(2)请写出图甲中所有的相似三角形(不含全等三角形)。
(3)如图乙,若以AB所在直线为 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为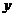 轴建立如图乙的平面直角坐标系,保持△ABD不动,将△ABC向
轴建立如图乙的平面直角坐标系,保持△ABD不动,将△ABC向 轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=
轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF= ,△FBP面积为
,△FBP面积为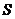 ,求
,求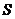 与
与 之间的函数关系式,并写出
之间的函数关系式,并写出 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com