
2007-2008学年度第二学期九年级期中质量检测
数学试卷
第Ⅰ卷 选择题(共36分)
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)
1.下列计算中,正确的是( ).
A.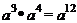 B.
B.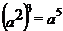 C.
C.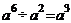 D.
D.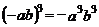
2.台湾是我国最大的岛屿,总面积为35989.76平方千米.用科学记数法应表示为(保留三个有效数字)( ).
A.3.59×105平方千米 B.3.60×106平方千米
C.3.59×104平方千米 D.3.60×104平方千米
3.函数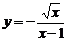 中自变量
中自变量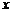 的取值范围是( )
的取值范围是( )
A.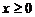 B.
B. C.
C.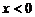 D.
D.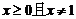
4.若 ,则
,则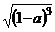 化简后为( )
化简后为( )
A.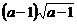 B.
B.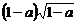 C.
C.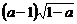 D.
D.
5.国家级历史文化名城――金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( ).

A.红花、绿花种植面积一定相等 B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等 D.蓝花、黄花种植面积一定相等
6.不等式组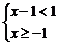 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )

7.小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( ).
分数
20
21
22
23
24
25
26
27
28
人数
2
4
3
8
10
9
6
3
1
A.该组数据的众数是24分 B.该组数据的平均数是25分
C.该组数据的中位数是24分 D.该组数据的极差是8分
8.如图,圆O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是( ).
A.3≤OM≤5 B.3≤OM<

9.如图,已知△ABC的面积为36,将△ABC沿BC平移到△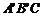 ,使
,使 和C重合,连结
和C重合,连结 变
变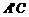 于D,则△
于D,则△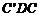 的面积为( ).
的面积为( ).
A.6 B.
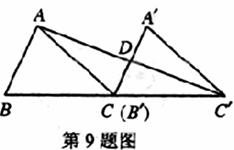
10.如图,矩形纸片ABCD中,AB=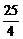 cm,则AD的长为( ).
cm,则AD的长为( ).
A.

11.均匀地向一个如图所示的容器中注水,最后把容器注满,在注水过程中水面高度h随时间t变化的函数图象大致是( ).

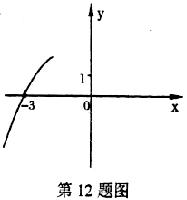
12.抛物线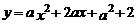 的一部分如图所示,那么该抛物线在
的一部分如图所示,那么该抛物线在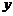 轴右侧与
轴右侧与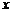 轴交点的坐标是( ).
轴交点的坐标是( ).
A.(0.5,0) B.(1,0) C.(2,0) D.(3,0)
第Ⅱ卷 非选择题(共84分)
二、填空题(本大题共5小题,共15分.只要求填写最后结果,每小题填对得3分.)
13.分式方程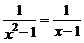 的解是____________.
的解是____________.
14.如图,矩形ABCD的边AB在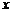 轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则a的取值范围是____________.
轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则a的取值范围是____________.

15.如图所示的圆柱体中底面圆的半径是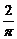 ,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是____________(结果保留根号).
,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是____________(结果保留根号).

16.如图,已知双曲线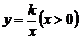 经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____________.
经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____________.

17.某水果公司以2元/千克的单价新进了10000千克柑橘,为了合理定出销售价格,水果公司需将运输中损失的水果成本折算到没有损坏的水果售价中.销售人员从柑橘中随机抽取若干柑橘统计柑橘损坏情况,结果如下表.如果公司希望全部售完这批柑橘能够获得5000元利润,那么在出售柑橘时,每千克大约定价____________元.
柑橘质量(千克)
50
200
500
损坏的质量(千克)
5.50
19.42
51.54
三、解答题(本大题共7题.共69分.解答应写出文说明、证明过程或推演步骤.)
18.(本题满分8分)
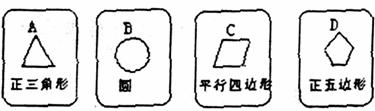
有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.
19.再一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行 )
)

20.(本题满分10分)
某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品.己知每件文化衫比每本相册贵9元,用200元恰好可以买到2件文化衫和5本相册.
(1)求每件文化衫和每本相册的价格分别为多少元?
(2)有几种购买文化衫和相册的方案?哪种方案用于购买老师纪念品的资金更充足?
21.(本题满分10分)
O点是△ABC所在平面内一动点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,如果DEFG能构成四边形.
(1)如图,当D点在△ABC内时,求证四边形DEFG是平行四边形;
(2)当O点移动到△ABC外时,(1)的结论是否成立?画出图形并说明理由;
(3)若四边形DEFG为矩形,O点所在位置应满足什么条件?试说明理由.

22.(本题满分10分)
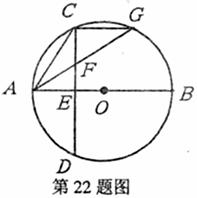
如图,己知AB是圆O的直径,弦CD上AB于E,F是CE上的一点,且FC=FA,延长AF交圆O于G,连结CG.
(1)试判断△ACG的形状(按边分类),并证明你的结论;
(2)若圆O的半径为5,OE=2,求CF?CD的值.
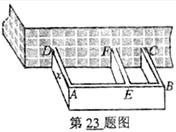
23.(本题满分11分)
某农户计划利用现有的一面墙再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为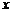 m,即AD=EF=BC=
m,即AD=EF=BC=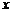 m.(不考虑墙的厚度)
m.(不考虑墙的厚度)
(1)若想水池的总容积为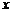 应等于多少?
应等于多少?
(2)求水池的总容积V与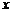 的函数关系式,并直接写出
的函数关系式,并直接写出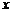 的取值范围;
的取值范围;
(3)若想使水池的总容积V最大,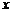 应为多少?最大容积是多少?
应为多少?最大容积是多少?
24.(本题满分12分)
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(―1,0),以AB的中点P为圆心,AB为直径作圆P与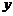 轴的正半轴交于点C.
轴的正半轴交于点C.
(1)求经过A、B、C三点的抛物线对应的函数表达式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数表达式;
(3)试说明直线MC与圆P的位置关系,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com