
2008年南京市白下区初中毕业生学业模拟考试(二)
数学试卷
考试时间120分钟 满分120分
下列各题所附的四个选项中,有且只有一个是正确的.
一、选择题(每小题2分,共20分)
1.一个数 a 的倒数是2,则 a 等于( )
A. 2
B. -
2.下列关于的说法中,错误的是( )
A.是无理数 B.=±
C.2<<3 D.=2
3.对于反比例函数y=-,下列说法正确的是( ).
A.它的图象在第一、三象限
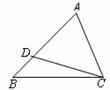
B.点(1,3)在它的图象上
C.当x>0时,y随x的增大而减小
D.当x<0时,y随x的增大而增大
4.下列一元二次方程中,有两个不相等的实数根的方程是( )
A.x2+5x+4=0 B.x2-2x+1=0
C.x2+4x+5=0 D.x2+1=0
5.数据-3,0,1,2,6的极差为( )
A.3 B.5 C.6 D.9
6.今年“五一”节,某商场举办有奖销售活动,办法如下:每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,凡购物满200元者可得奖券一张,多购多得,那么买200元商品的中奖概率应该是( )
A. B. C. D.
7.如图,一次函数的图象经过点A、B,则该一次函数的关系式为( )
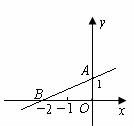
A.y=-x+1 B.y=x+1
C.y=-2x+1 D.y=2x+1
8.若∠α的余角是30°,则sinα等于( )
A. B. C. D.1
9.如图,小明从O点出发,先向西走40米,再向南走30米到达点M,如果点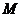 的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
的位置用(-40,-30)表示,那么(-10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
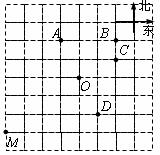
10.如图,⊙O内切于正△ABC,正△DEF内接于⊙O,则S△DEF :S△ABC等于( )
A.1:2 B.1:3 C.1:4 D.1:5
二、填空题(每小题3分,共18分)
11.如果式子在实数范围内有意义,那么x的取值范围是 .
12.李老师设计了一个计算程序,输入和输出的数据如下表:
输入数据
1
2
3
4
5
…
输出数据
-
-
-
…
那么,当输入数据为6时,输出的数据是 .
13.如图,在△ABC中,AB>AC,点D在AB边上,若再增加一个条件就能使△ABC∽△ACD,则这个条件可以是 .
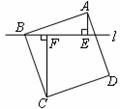
14.如图,直线l过正方形ABCD的顶点B,过A、C分别作l的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为 .
15.某班有学生36人,其中男生比女生的2倍少6人.如果设该班男生有x人,女生有y人,那么可列方程组为 ,
,
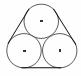
16.如图是被铁丝捆绑在一起的三根底面半径为50cm的圆柱的横截面,那么至少需要长为
cm的铁丝.(接头捆扎部分不算,结果保留π)
三、(每小题6分,共18分)
17.计算:-b(a≥0,b>0).
18.解不等式组 并把它的解集在数轴上表示出来.
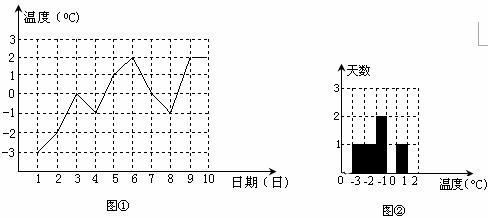
19.如图①是某城市三月份1至10日每天的最低气温随时间变化的折线统计图.
(1)根据图①提供的信息,在图②中补全直方图;
(2)这10天最低气温的众数是_______℃,最低气温的中位数是_______℃,最低气温的平均数是______℃.
四、(每小题6分,共18分)
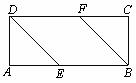
20.如图,在矩形ABCD中,AB=4,AD=2,E、F分别是边AB、CD上的点,且BE=DF,连接BF、DE.
(1)求证:四边形DEBF是平行四边形;
(2)当AE的长为多少时,四边形DEBF是菱形?
21.有两个信封,每个信封内各装有三张卡片,其中一个信封内的三张卡片上分别写有1,2,3三个数,另一个信封内的三张卡片上分别写有4,5,6三个数.甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于10,则甲获胜,否则乙获胜.
(1)请你通过画树状图(或列表)计算甲获胜的概率;
(2)你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请修改游戏规则,使其公平.
22.某校科技小组进行野外考察,途中遇到一片的烂泥湿地.为了人员和设备安全迅速地通过这片湿地,他们沿着前进路线铺了若干块大小不同的木板,构筑成一条临时通道.已知当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
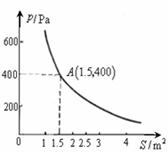
(1)请直接写出p与S之间的关系式和自变量S的取值范围;
(2)当木板面积为0.2 m2时,压强是多少?
五、(每小题7分,共14分)
23.如图,在平面直角坐标系中,B点在x轴上,∠AOB=60°,线段OA=6.将△AOB绕点O逆时针旋转60°后,点A落在C点处,点B落在D点处.
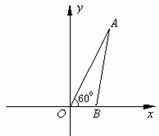
(1)请在图中画出△COD(不写画法),并在所画图中标出C点的坐标;
(2)求A点在旋转过程中所经过的路程的长.(结果保留整数)
24.某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,其关系式为:w=-2x+240.如果物价部门规定这种绿茶的销售单价不得高于90元/千克,该公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
六、(每小题7分,共14分)
25.如图,一艘轮船位于灯塔P的北偏东45°方向,距灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东35°方向上的B处.这时,轮船所在的B处距离灯塔P有多远?(精确到0.1海里)(参考数据:≈1.41,≈1.73,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)

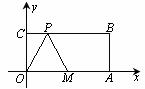
26.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),M是OA的中点,点P在BC边上运动.
(1)当PO=PM 时,点P的坐标为 ;
(2)当△OPM是腰长为5的等腰三角形时,求点P的坐标.
七、(本题8分)
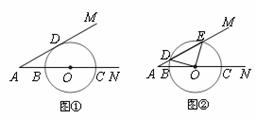
27.已知∠MAN=30°,点O在AN上,以O为圆心,6 为半径作⊙O ,交AN于B、C两点.
(1)如图①,当⊙O 与AM 相切于点D 时,求线段AB 的长;
(2)如图②,当⊙O与AM 相交于D、E 两点,且∠DOE=90° 时,求线段AB的长.
八、(本题10分)
28.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点P从O点出发,以每秒2个单位长度的速度向A运动,同时点Q从B点出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停止运动.过点Q作QD⊥x轴,垂足为点D,交AC于点E.
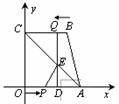
(1)求△APE的面积 S 与运动时间 t(单位:秒) 的函数关系式,并写出自变量 t 的取值范围;
(2)当t 为何值时,S 的值最大;
(3)是否存在点P,使得△APE为直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com