
2008年南京市高淳县初中毕业生学业模拟考试(二)
数学试卷
注意事项:
一、选择题(下列各题所附的四个选项中,有且只有一个是正确的,每小题2分,共20分)
1.如果a与-2互为倒数,那么a是( )
A.-2
B.-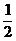 C.
C.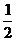 D.2
D.2
2.大多数细菌的直径在0.5~5微米(1微米=10-
A.0.7×10―
3.不等式x+3>0的解集在数轴上表示正确的是( )

4.在函数y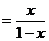 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A.x≠1 B.x≠
5.下列图形中,既是中心对称图形又是轴对称图形的是( )
A.等边三角形 B.菱形 C.等腰梯形 D.平行四边形
6.如图:把一个转盘等分成六个小扇形,小明想把其中的几个小扇形涂成红色,使得随机转动转盘后,指针落在红色区域的概率为,则小明应将其中的几个小扇形涂成红色?( )
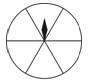
A.1
B.
7.下面四个几何体中,主视图、左视图、俯视图是全等图形的几何体是( )
A.正方体 B.圆柱 C.三棱柱 D.圆锥
8.如图,AB是⊙O直径,∠D = 35°,则∠BOC的度数为( )
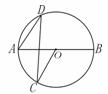
A.120° B.70°
C.100° D.110°
9.给出以下三个命题:
①对角线相等的四边形是矩形;
②一条对角线平分一个内角的平行四边形是菱形;
③一组对边平行,另一组对边相等的四边形是平行四边形.其中真命题有( )
A.0个 B.1个 C.2个 D. 3个
10.如图1,把圆形井盖卡在角尺(角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移
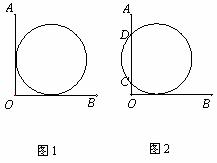
A.
C.
二、填空题(每小题3分,共18分)
11.方程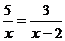 的解为 .
的解为 .
12.将命题“等腰三角形的两个底角相等”改写为“如果……,那么……”的形式:
如果 ,那么 .
(写一个满足条件的k的值即可)
13.如果反比例函数 的图象经过二、四象限. 那么k的值可以是 .
的图象经过二、四象限. 那么k的值可以是 .
14.学校广播站要招聘一名记者,小明、小亮报名参加了3项素质测试,成绩如下:
采访写作
计算机
创意设计
小明
70分
70分
85分
小亮
90分
75分
60分
把采访写作、计算机、创意设计成绩按5┱2┱3的成绩计算两个人的素质测试平均成绩,那么,谁将被录取?答: .
15.如图,扇形OAB的圆心角为直角,正方形OCDE的顶点分别在OA、OB、弧AB上,AF⊥ED,交ED的延长线于点F,如果正方形的边长为1,图中阴影部分面积为 .
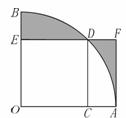
16.如图,在平面直角坐标系中,O为坐标原点,四边形 OABC 是矩形,点B坐标分别为 (5,4),点P为BC上动点,当△POA为等腰三角形时,点P点坐标为 .
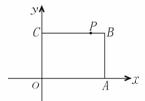
三、(第17、18、19题每小题6分,第20题7分,共25分)
17.计算: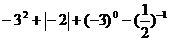
18.先化简,再求值.
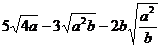 (a≥0,b>0),其中a=2,b=8.
(a≥0,b>0),其中a=2,b=8.
19.为了了解全县12000名中学生体育的达标情况,现从七、八、九年级学生中共抽查了1000名学生的体育达标情况作为一个样本,制作了各年级学生人数分布情况、各年级达标人数的两张统计图.
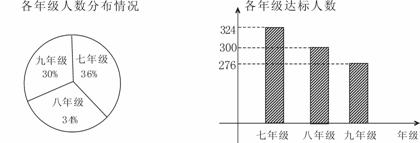
(1)样本中七年级学生共有 人,七年级学生的体育达标率为 ;
(2)三个年级学生中体育达标率最高的是那个年级?答: ;
(3)估计全县体育达标的学生人数有多少人.
20.团体购买公园门票的价格如下表所示:
购票人数
1~50人
51~100人
100人以上
票价
10元/人
8元/人
6元/人
今有甲、乙两个旅行团,其中甲团不足50人,乙团超过50人但不足100人.如果两团分别购票,一共要付门票费908元;如果两个团合在一起作为一个团体购票,一共要付612元.
⑴判断两团总人数是否超过100人?说明理由;
⑵求甲、乙两旅行团分别有多少人.
四、(第21、22题每题6分,第23题7分,共19分)
21.如图,△ABC中,∠BAC=45°,高AD、CE相交于点H.
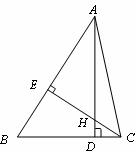
⑴求证:BE=EH ;
⑵若AE=4,BE =3,求CH的长
22.如图,△ABC为网格中的格点三角形.
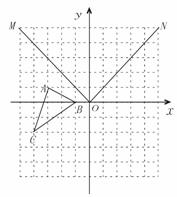
(1).画出图形
?.△ABC关于y轴所在直线对称的△A1B
(2)填空:
下列哪些变换可使△A2B
①将△A2B
②将△A2B
③先将△A2B
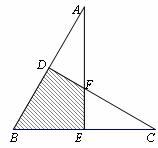
23.将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=
∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
五、(第24题7分,第25题6分,共13分)
24.家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温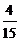 kΩ.
kΩ.

⑴求当10≤t≤30时,R和t之间的关系式;
⑵求温度在
⑶家用电灭蚊器在使用过程中,温度在什么范围内时, 发热材料的电阻不超过6 kΩ?
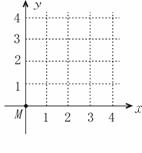
25.位于坐标原点的一个质点M按下列规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的可能性相同.
①列出质点M移动3次时所有可能的方法,并用坐标表示出它的位置;
②求质点M移动3次后位于点(1,2)的概率.
六、(本题8分)
26.如图:已知二次函数y=ax2-x+a+2过点A(1,0),
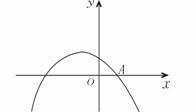
(1)求a的值;
(2)写出该函数图象的顶点坐标;
(3)代数式ax2-x+a+2的值可取到哪几个正整数?求出它取正整数时所对应的x的值.(要求写出求解过程)
七、(本题8分)
27.已知:如图,△ABC中,以AB为直径的⊙O交AC于点D,且 D为AC的中点,过D作DE⊥CB,垂足为E.
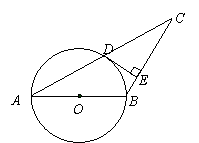

(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)已知CD=4,CE=3, 求⊙O的半径.
八、(本题9分)
我们知道二元一次方程组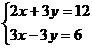 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组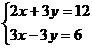 有唯一解.
有唯一解.
我们也知道二元一次方程2x+3y=12的解有无数个,而在实际问题中我们往往只需要求出其正整数解.
下面是求二元一次方程2x+3y=12的正整数解的过程:
由2x+3y=12得:y=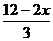 =4-
=4-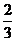 x
x
∵ x、y为正整数, ∴
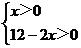 则有0<x<6
则有0<x<6
又y=4-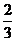 x为正整数,则
x为正整数,则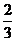 x为正整数,所以x为3的倍数.
x为正整数,所以x为3的倍数.
又因为0<x<6,从而x=3,代入:y=4-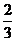 ×3=2
×3=2
∴2x+3y=12的正整数解为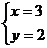
问题:⑴若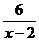 为正整数,则满足条件的x的值有几个. ( )
为正整数,则满足条件的x的值有几个. ( )
A.2
B.
⑵九年级某班为了奖励学习进步的学生,花费35元购买了笔记本和钢笔两种奖品,其中笔记本的单价为3元/本,钢笔单价为5元/支,问有几种购买方案?
⑶试求方程组
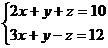 的正整数解.
的正整数解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com