
2008年南京市鼓楼区九年级第二次模拟调研测试
数学试卷
满分120分 考试时间120分钟
下列各题所附的四个选项中,有且只有一个是正确的.
一、选择题(每小题2分,共20分)
1.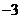 的倒数是
( )
的倒数是
( )
A.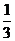 B.
B.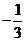 C.
C.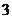 D.
D.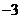
2.计算(a3b)2结果正确的是 ( )
A.a9b B.a9b
3.某班45名同学的年龄分布情况如图所示,则该班学生年龄的众数是 ( )

A.12 B.13 C.15 D.20
4.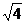 的值为
( )
的值为
( )
A. ±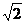 B.
B. 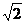 C. ±2
D. 2
C. ±2
D. 2
5.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A.148(1+a%)2=200 B.200(1-a%)2=148
C.200(1-2a%)=148 D.200(1-a2%)=148
6.二次函数y=x2+2x-1的最小值是 ( )
A.-1 B.-2 C.1 D.2
7.在△ABC中,若∠C=90°,cosA= ,则∠A等于 ( )
A. 30° B. 45° C. 60° D. 90°
8.如图,已知点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,
点B的坐标为 ( )
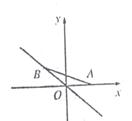
A.(0,0)
B.(1,-1 C.(,-) D.(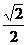 ,
, )
)
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa )是气体体积V( m3 ) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.那么,使气球爆炸的体积范围是 ( )
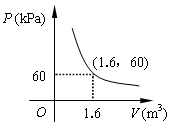
A.不小于 m3 B.小于
m3 B.小于 m3 C.不小于
m3 C.不小于 m3 D.小于
m3 D.小于 m3
m3
10.定义:定点P与⊙O上的任意一点之间的距离的最小值称为点P与⊙O之间的距离.
现有一矩形ABCD(如图),AB=14cm,BC=12cm,⊙K与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙K的距离为 ( )
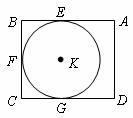
A.4cm B.8cm C.10cm D.12cm
二、填空题(每小题3分,共18分)
11.投掷一枚骰子,得到正面朝上的数字是3的概率是 .
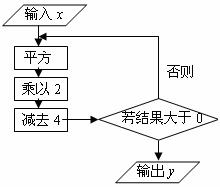
12.根据如图所示的程序计算,若输入x的值为1,则输出y的值为 .
13.一次函数的图象过点(1,2),且函数值y随着自变量x的增大而减小,写出一个符
合这个条件的一次函数的表达式: .
14.根据下表中的规律,表中的空格中应填写的数字是 .




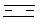
000
110
010
100
111
001
101
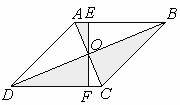
15.如图,菱形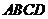 的对角线
的对角线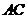 和
和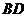 相交于点
相交于点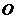 ,过点
,过点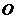 的直线分别交AB和CD于点E、F,BD=6,AC= 4,则图中阴影部分的面积和为 .
的直线分别交AB和CD于点E、F,BD=6,AC= 4,则图中阴影部分的面积和为 .
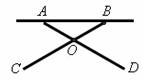
16.如图是一张简易活动餐桌平放在地面上,如果两条桌腿的张角(∠COD)为120°,OA=OB,OC=OD,桌面离地面的高度为70cm(不考虑桌面厚度),那么桌腿AD长应为
cm.
三、(每小题6分,共24分)
17.化简: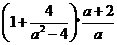 .
.
18.求不等式组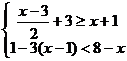 的整数解.
的整数解.
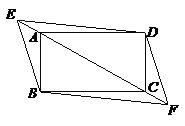
19.如图,在矩形ABCD中,点E、F分别在CA、AC的延长线上,且AE=CF.请确定
四边形BEDF的形状,并证明你的结论.
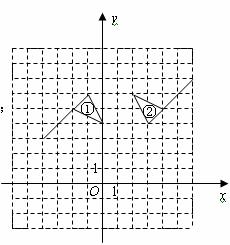
20.如图,在平面直角坐标系中,图形①与图形②关于点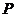 成中心对称.
成中心对称.
(1)画出对称中心 ,并写出点
,并写出点 的坐标;
的坐标;
(2)将图形②向下平移4个单位,画出平移后的图形③;
⑶请具体说明图形③经过怎样变换可直接得到图形①.
四、(第21题5分,第22题6分,共11分)
21.下表是某居民小区五月份的用水情况:
月用水量(米3)
4
5
6
8
9
11
户数
2
3
7
5
2
1
(1)计算20户家庭的月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计这500户家庭该月共用水多少立方米?
22.农历正月十五元宵节有吃汤元的习俗.小华的妈妈在包的48个汤元中,有两个汤元用红枣做馅,与其它汤元不同馅.现每碗盛8个汤元,共盛6碗,且两个红枣汤圆被盛到不同的碗里,若小华吃2碗,则吃到包有红枣的汤元,.
(1)小华吃的两碗中都有红枣汤元的概率;
(2)小华吃到红枣汤元的概率.
五、(第23题7分,第24题8分,共15分)
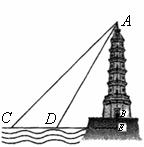
23.某中学数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔 的高度.如图,在湖面上点
的高度.如图,在湖面上点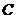 测得塔顶
测得塔顶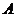 的仰角为
的仰角为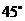 ,沿直线
,沿直线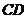 向塔
向塔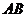 方向前进
方向前进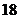 米到达点
米到达点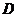 ,测得塔顶
,测得塔顶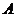 的仰角为
的仰角为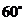 .已知湖面低于地平面
.已知湖面低于地平面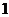 米,请你帮他们计算出塔
米,请你帮他们计算出塔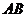 的高度.(结果精确到0.1 米,参考数据:≈1.41,≈1.73)
的高度.(结果精确到0.1 米,参考数据:≈1.41,≈1.73)
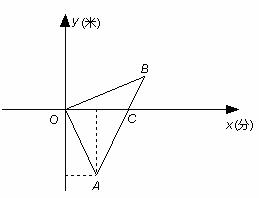
24.早晨小明与妈妈同时从家里出发,步行与骑自行车到方向相反的两地上学与上班.妈妈骑车走了一会接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达校.他们离家的路程 y (米)与时间 x (分)的函数图象如图所示.
已知A点坐标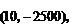
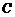 点坐标为
点坐标为 .
.
(1)在图中,小明离家的路程 y (米)与时间 x (分)的函数图象是线段
(A)OA (B)OB (C)OC (D)AB
(2)分别求出线段OA与AB的函数表达式(不需要写出自变量的取值范围);
(3)已知小欣步行速度为每分50米,则小欣家与学校距离为 米,小欣早晨上学需要的时间 分钟.
六、(每题7分,共14分)
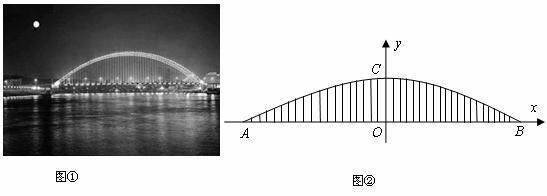
25.图①中是一座下承式钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,拱肋的跨度AB为280米,正中间系杆OC的长度为56米。以AB所在直线为x轴,OC所在直线为y轴建立如图②所示的平面直角坐标系。
(1)求与该抛物线对应的函数关系式;
(2)若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由。
26.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设正n边形的每个内角的度数为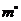 ,将正n边形的“接近度”定义为
,将正n边形的“接近度”定义为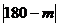 .于是,
.于是,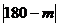 越小,该正n边形就越接近于圆.
越小,该正n边形就越接近于圆.
①若n=20,则该正n边形的“接近度”等于 ;
②当“接近度”等于 时,正n边形就成了圆.



(2)设一个正n边形的半径(即正n边形外接圆的半径)为R,边心距(即正n边形的中心到各边的距离)为r,将正n边形的“接近度”定义为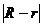 ,于是
,于是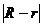 越小,正n边形就越接近于圆.你认为这种说法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
越小,正n边形就越接近于圆.你认为这种说法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
七、(本题8分)
27.小明家新买了一辆小汽车,可是小区内矩形停车场ABCD只有9个已停满车的车位(图1中的小矩形APQR等),该矩形停车场的可用宽度(CD)只有5米.由于种种原因,车位不能与停车场的长边BC垂直设计.为了增加车位,小明设计出了图2的停车方案,每个车位(图2中的小矩形EFGH等)与该停车场的长边的夹角为37°,且每个车位的宽与原来车位保持不变,每个车位的长比原来车位少1米.这样,总共比原来多了3个车位.设现在每个车位的长为x米,宽为y米.
(参考数据:sin37°=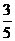 ,cos37°=
,cos37°=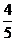 ,tan37°=
,tan37°= .)
.)
(1)请用含x的代数式表示BE;用含y的代数式表示AH;
(2)求现在每个车位的长和宽各是多少米?




八、(本题10分)
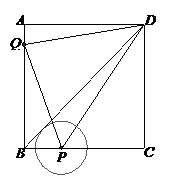
28.如图,已知正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度沿B→C→D方向,向终点D运动;动点Q从点A出发,以1cm/s的速度沿A→B方向,向终点B运动.若P、Q两点同时出发,运动时间为ts.
(1)当t= s时,P到达终点D;
(2)当点P在BC上运动时,是否存在这样的t,使得PD=QD?若存在,请求出符合条件的t的值;若不存在,请说明理由;
(3)以点P为圆心,作⊙P,使得⊙P与对角线BD相切.问:在点P的运动过程中,是否存在这样的t,使得⊙P恰好经过正方形ABCD的某一边的中点?若存在,请写出符合条件的t的值;若不存在,请说明理由.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com