
2008年南京市溧水县第二学期初三第二次调研测试
数学试卷
一、选择题(每小题2分,共20分)
1.计算│-2│-2的结果是( ).
A.0 B.-
2.计算x 6÷x 3的结果是( ).
A. x 9 B. x
3.一次数学测试后,随机抽取九年级二班5名学生的成绩如下:78,85,91,98,98.关于这组数据说法错误的是( ).
A.极差是20 B.众数是
4.从某班学生中随机选取一名学生是女生的概率为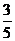 ,则该班女生与男生的人数比是( ).
,则该班女生与男生的人数比是( ).
A.3∶2 B.3∶5 C. 2∶3 D.2∶5
5.不等式组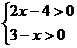 的解集为( ).
的解集为( ).
A.x>2 B.x<3 C.x>2或 x<-3 D.2<x<3
6.抛物线y = x2 -1的顶点坐标是( ).
A.(0,1) B.(0,-1) C.(1,0) D.(-1,0)
7.如果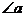 是等边三角形的一个锐角,则
是等边三角形的一个锐角,则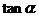 的值是( ).
的值是( ).
A.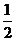 B.
B.
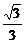 C.
C.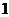 D.
D.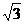
8.如下图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( ).
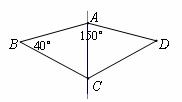
A.130° B.150° C.40° D.65°
9.若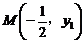 ,
,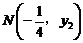 ,
,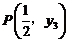
 三点都在函数
三点都在函数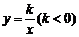 的图象上,
的图象上,
则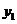 、
、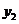 、
、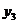 的大小关系为( ).
的大小关系为( ).
A.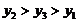 B.
B.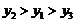 C.
C.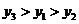 D.
D.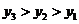
10.如下图,在平面直角坐标系中,圆心在x轴上的⊙E与两坐标轴分别交于A、B、C、D四点,已知A(-1,0),B(9,0),则线段CD的长度为( ).
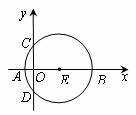
A.3 B.4 C.6 D.8
二、填空题(每小题3分,共18分)
11.因式分解:2m2-8 = .
12.要使二次根式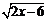 有意义,
有意义,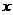 应满足的条件是__________.
应满足的条件是__________.
13.将一副直角三角尺如图放置,则∠ABC= °.
14.已知某个几何体的主视图、左视图、俯视图分别为三角形、三角形、圆,则该几何体是
.
15.已知圆锥的底面半径为9┩,母线长为30┩,则圆锥的侧面积为 (结果保留π).
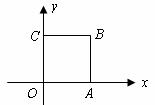
16.如图,正方形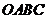 的边长为2,则该正方形绕点
的边长为2,则该正方形绕点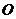 逆时针旋转
逆时针旋转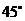 后,
后,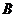 点的坐标为 .
点的坐标为 .
三、(每小题5分,共15分)
17.计算: 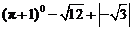 .
.
18.解方程: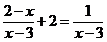 .
.
19.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,
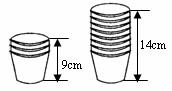
(1)求整齐叠放纸杯的高度y(cm)与纸杯数x(个)之间的一次函数关系式;
(2)若小明把50个纸杯整齐叠放在一起时,它的高度是多少?
四、(第20、21、22题,每小题6分,第23题7分,共25分)
20.在“五?一”期间,小明、小亮等同学随家人一同到某旅游景点游玩.下表是该旅游景点的票价情况
票价
成人
40元/张
学生
按成人票价的5折优惠
小明他们13个人,共需420元,问小明他们一共去了几个成人?几个学生?
21.《中学生体质健康标准》规定学生体质健康等级标准为:86分及以上为优秀;76分~85分为良好;60分~75分为及格;59分及以下为不及格.某校从九年级学生中随机抽取了10%的学生进行了体质测试,得分情况如下图.
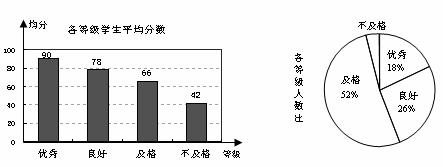
(1)在抽取的学生中不及格人数所占的百分比是 ;
(2)若抽取的学生中优秀的人数有9人,请算出共抽取了多少名学生?
(3)小明按以下方法计算出抽取的学生平均得分是:(90+78+66+42)÷4=69.根据所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式;(不必算出结果)
22.甲、乙两人组队参加一次竞猜游戏活动,活动中抽到一道选择题,有A、B、C三个选项,只有选项B是正确答案.甲、乙两人都不知道正确答案,两人各任意猜一个答案,若规定两人答案都正确得3分,两人中有且只有一个人的答案正确得1分,两人答案都不正确得0分.回答下列问题:
(1)两人该题得3分的概率是多少?
(2)两人该题得1分的概率是多少?
23.已知,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与BC相切于M,与AB、AD分别相交于E、F.
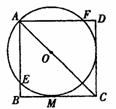
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为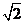 ,求正方形ABCD的边长.
,求正方形ABCD的边长.
五、(第24题7分,第25题8分,共15分)
24.如图,在 中,
中,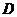 是
是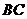 边上的一点,
边上的一点,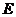 是
是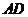 的中点,过
的中点,过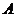 点作
点作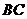 的平行线交
的平行线交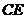 的延长线于
的延长线于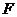 ,且
,且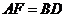 ,连结
,连结 .
.
(1)求证: 是
是 的中点.
的中点.
(2)如果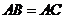 ,试判断四边形
,试判断四边形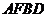 的形状,并证明你的结论.
的形状,并证明你的结论.
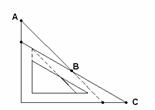
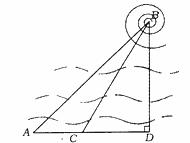
25.如下图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救。1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑300m到离B点最近的D点,再跳入海中.救生员在岸上跑的速度都是6m/s,在水中游泳的速度都是2m/s.若∠BAD= 45°,∠BCD=60°,三名救生员同时从A点出发,请说明谁先到达营救地点B. (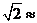 1.4,
1.4,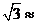 1.7)
1.7)
六、(8分)
26.我们知道,用一块直角三角板就可以过一点画一条直线的垂线.
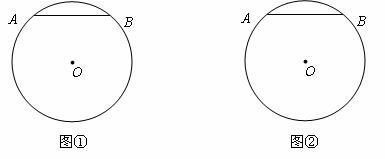
如图,AB是⊙O的弦,现在只有一块无刻度单位的直角三角板(斜边大于⊙O的直径),请你用两种不同的方法分别在图①、图②中确定出弦AB中点的位置(画出图形,标出直角),并且分别写出画图的步骤(不要证明).
七、(本题8分)
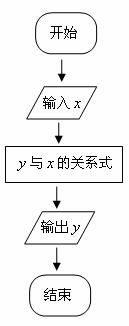
27.按下图所示的流程,输入一个数据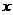 ,根据
,根据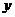 与
与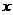 的关系式就输出一个数据
的关系式就输出一个数据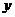 ,这样可以将一组数据变换成另一组新的数据.要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
,这样可以将一组数据变换成另一组新的数据.要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(i)新数据都在60~100(含60和100)之间;
(ii)新数据之间的大小关系与对应的原数据之间的大小关系一致,即原数据大的对应的新数据也较大.
(1)若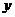 与
与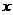 的关系式是
的关系式是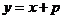
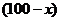 ,请说明:当
,请说明:当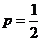 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式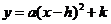 (
(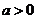 )将数据进行变换,请写出一个满足上述要求的这种关系式.并利用函数性质说明你所写函数关系式满足上述要求.
)将数据进行变换,请写出一个满足上述要求的这种关系式.并利用函数性质说明你所写函数关系式满足上述要求.
八、(本题11分)
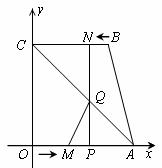
28.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点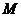 从
从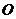 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向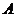 运动;点
运动;点 从
从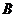 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向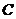 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点 作
作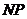 垂直
垂直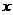 轴,垂足为
轴,垂足为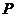 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
(1)点______(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com