
2008年南京市六合区初三第二次模拟测试
数学试卷
一、选择题(每小题2分,共20分)
1. 的相反数为( ).
A. 2 B.-
2.下列各图中,中心对称图形是( ).

A. B. C. D.
3.9的平方根等于( ).
A.3
B.
-
4.下图是一个正方体的平面展开图,当把它围成一个正方体后,与空白面相对面上的字应该是( ).
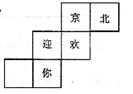
A.北 B.京 C.欢 D.迎
5.对于函数y=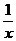 ,当x≥2时,相应函数值y的范围是( ) .
,当x≥2时,相应函数值y的范围是( ) .
A.y≥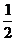 B.y≤
B.y≤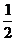 C.y>
C.y>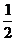 D.0<y≤
D.0<y≤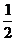
6.若二次函数y=x2-2x-m的图象的顶点在x轴上,则m的取值范围是( )
A.m <-1 B. m <
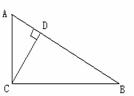
7.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,则sin∠ACD的值为( ).
A.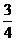 B.
B.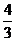 C.
C.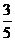 D.
D.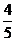
8.苏通大桥全长
A.1.296┩ B.12.96┩ C.0.81┩ D.8.1┩
9.某“中学生环保小组”的同学随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区1200户家庭一周内需要环保方便袋约( )
A.84000只 B.8400只 C.12000只 D.1200只
10.如图,⊙O在长为
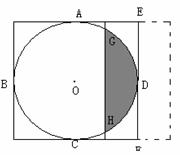
A.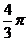 B.
B.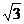 C.
C.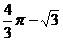 D.
D.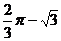
二、填空题(每小题3分,共18分)
11.计算: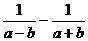 =
.
=
.
12.袋中装有3个红球、2个黄球、1个白球,现从袋中任意摸出1个球,摸出黄球的概率为 .
13.如下图,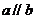 ,直线c与两条已知直线交于点A ,B,过点A作直线b的垂线,垂足为点C.若∠1=130°,则∠2=
°.
,直线c与两条已知直线交于点A ,B,过点A作直线b的垂线,垂足为点C.若∠1=130°,则∠2=
°.
14.伴随着社会经济的全面发展,南京市的人口规模不断扩大。2007年末全市常住人口约为741.3万人,用科学记数法表示为 人(保留两位有效数字).
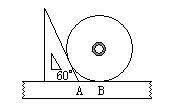
15.如下图,小明同学用一把直尺和一块三角板测量一个光盘的直径,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=
16.如下图,边长为2的等边△ABC在平面直角坐标系中,边BC与x轴平行,若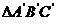 与△ABC关于x轴对称,则点A′的坐标是
.
与△ABC关于x轴对称,则点A′的坐标是
.
三、(每小题6分,共18分)
17.计算: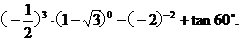
18.解方程: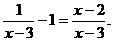
19.如下图,△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系:①AD=BC; ②DE=CF; ③BE∥AF
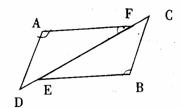
(1)请用其中两个关系作为条件,另一个作为结论,写出一个你认为正确的命题.你选择的条件为: ,结论为: .
(2)请证明你所选择的命题。
四、(第20题6分,第21题6分,第22题7分,第23题6分,共25分)
20.袋中放有08年北京奥运会吉祥物五福娃(贝贝、晶晶、欢欢、迎迎、妮妮)纪念币一套,依次取出(不放回)两枚纪念币,求取出的两枚纪念币中恰好有一枚是“欢欢”的概率是多少?
21.今年我国部分地区发生了“手足口”病情,这是一种肠道传染病,其主要是通过接触被感染的手、食品及生活用品等引起感染.小军和他的同学在小区里开展了一次安全卫生宣传,并抽样调查了居民 对“手足口”病的了解情况,结果如下:
了解程度
A 比较了解(知道传染途径和预防措施)
B 一般了解(只知道是传染
病,但途径和预防不清楚)
C 不了解(没有关注,不清楚是什么)
人数
30
40
※
根据抽样调查结果回答下列问题:
(1)请将B,C标注在扇形统计图对应的区域中,本次抽样调查中,“不了解”(即C)的人数是 人;
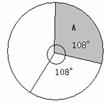
(2)若小区有居民约5000人,根据抽样调查,试估计该小区约有多少人对“手足口”这一病情“比较了解”(即 A)?
22.今年5月12日,四川省川县发生里氏7.8级地震.我市紧急调运食品30吨、日用品13吨支援灾区,现计划安排甲、乙两种货车共10辆将这批急需品全部运往灾区。已知甲种货车可同时装载食品4吨和日用品1吨,乙种货车可同时装载食品、日用品各2吨。甲、乙两种货车各需多少辆?
23.如图,已知∠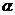 和线段m.求作:△ABC,使得AB=AC=m,∠B=∠
和线段m.求作:△ABC,使得AB=AC=m,∠B=∠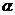 .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
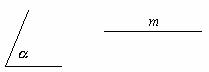
五、(第24题7分,第25题8分,共15分)
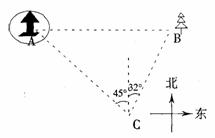
24.如下图,某风景区的湖心小岛上有一凉亭A,其正东方有一棵大树B,小明想测量A、B间的距离。他从湖边的C处测得A在北偏西45°的方向.测得B在北偏东32°的方
向,且量得B、C之间的距离为
25.如下图,点P是⊙O外一点,PO交⊙O于点C,PO=5,点A是⊙O上一点,过点A作AH⊥OP于点H,交⊙O于点B,AB=4.8,HC=1.2,
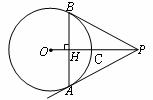
(1)求⊙O的半径;
(2)当PA为多少时,PA与⊙O相切?请说明理由.
六、(本题8分)
26.施工队要修建一个横断面为抛物线的公路隧道,其高度为
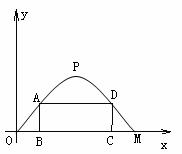
(1)求出这条抛物线的函数解析式;
(2)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.设OB长为k.
①用k表示出“脚手架”三根支架AB、AD、DC的长;
②三根支架AB、AD、DC的长度之和的最大值是多少?
注:二次函数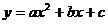 图象的顶点坐标为 (
图象的顶点坐标为 (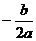 ,
,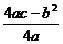 )
)
七、(本题8分)
为解方程 ,我们可以将
,我们可以将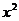 看作一个整体,设
看作一个整体,设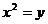 ,则原方程可化为
,则原方程可化为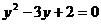 ,解得
,解得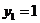 ,
,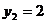 。当
。当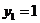 时,
时,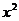 =1,∴
=1,∴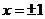 ;当
;当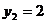 时,
时,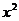 =2,∴
=2,∴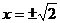 。因此原方程的解为:
。因此原方程的解为: 。
。
(1)已知方程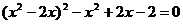 ,如果设
,如果设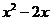
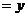 ,那么原方程可化为 。
,那么原方程可化为 。
28.已知,如图,四边形AOBC是正方形,点C的坐标是(4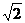 ,0),动点P沿折线OACB方向运动,运动速度是每秒1个单位长.Q沿折线OBCA方向运动,运动速度是每秒2个单位长,运动到相遇时停止。
,0),动点P沿折线OACB方向运动,运动速度是每秒1个单位长.Q沿折线OBCA方向运动,运动速度是每秒2个单位长,运动到相遇时停止。

(1)设△PQO的面积为S,运动时间为t秒,求S与t的函数关系式。
(2)当t为何值时,以A,P,B,Q四点为顶点的四边形是平行四边形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com