
2008-2009学年度潍坊市诸城第一学期八年级诊断题
数学试卷
(时间:120分钟)
一、选择题(每小题3分,共42分)
1.|一4|的算术平方根是( )
A.4 B.一
2.下列运算正确的是( )
A.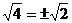 B.
B.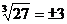 C.
C.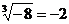 D.-|-2|=2
D.-|-2|=2
3.在实数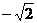 ,
,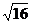 ,
,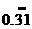 ,
,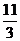 ,
,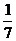 ,
,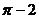 中,无理数的个数为( )
中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
4.一个正数的两个平方根分别是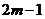 和
和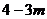 ,则这个数是( )
,则这个数是( )
A.3 B.
5.下列计算正确的是( )
A.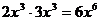 B.
B.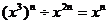
C.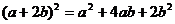 D.
D.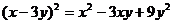
6.下面计算中,能用平方差公式的是( )
A.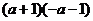 B.
B.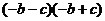
C.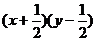 D.
D.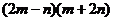
7.下列各式中,运算结果为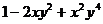 的是( )
的是( )
A.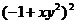 B.
B.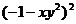
C.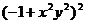 D.
D.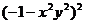
8.下列各式能用完全平方公式分解因式的是( )
A. B.
B.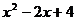 C.
C.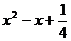 D.
D.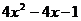
9.已知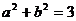 ,
,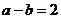 ,那么
,那么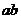 的值是( )
的值是( )
A.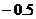 B.0.
B.0.
10.已知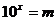 ,
,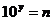 ,则
,则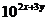 等于( )
等于( )
A.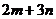 B.
B.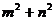 C.
C.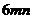 D.
D.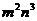
11.若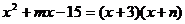 ,则m的值为( )
,则m的值为( )
A.一5 B.
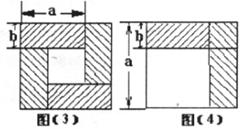
12.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(3)可以用来解释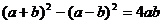 .那么通过图(4)面积的计算,验证了一个恒等式,此等式是( )
.那么通过图(4)面积的计算,验证了一个恒等式,此等式是( )
A.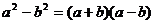 B.
B.
C.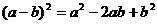 D.
D.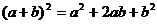
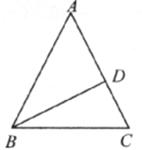
13.如图,△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BC等于( )
A.2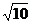 B.
B.
14.下图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是( )

A.13 B.
二、填空题(每小题3分,共24分)
1.当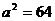 时,
时,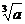 =_____________.
=_____________.
2.若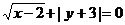 ,则
,则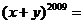 _____________.
_____________.
3.计算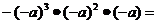 ______________.
______________.
4.计算: __________;
__________;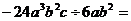 ____________.
____________.
5.若 的计算结果中
的计算结果中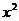 项的系数为一3,则m=___________.
项的系数为一3,则m=___________.
6.若整式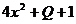 是完全平方式,请你写一个满足条件的单项式Q是____________.
是完全平方式,请你写一个满足条件的单项式Q是____________.
7.已知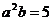 ,则
,则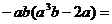 ____________.
____________.
8.若等腰直角三角形斜边长为2,则它的直角边长为____________.
三、简答题
1.计算:(每小题3分,共12分)
(1)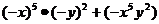 (2)
(2)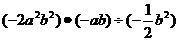
(3)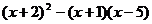 (4)
(4)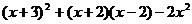
2.先化简再求值:(每题6分,共12分)
(1)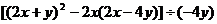 ,其中
,其中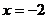 ,
,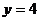 .
.
(2)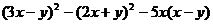 ;其中
;其中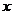 =2,
=2,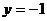 .
.
3.把下列多项式分解因式(每小题2分,共8分)
(1)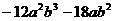 (2)
(2)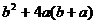
(3)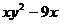 (4)
(4)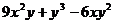
4.(本题6分)
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.
如:4=22-02、12=42-22、20=62-42,因此4,l2,20都是“神秘数”
①28是“神秘数”,为什么?
②设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数,为什么?
③两个连续正奇数的平方差与4的差(取正数)是神秘数吗?________(只要填“是”或“不是”)
5.解决问题(6分)
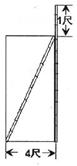
有一个小朋友拿着一根竹竿通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜入就恰好等于门的对角线长,已知门宽4尺。请求竹竿高与门高。
6.解决问题(10分)
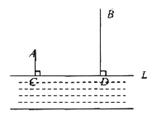
如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com