
2007-2008学年度烟台市招远第二学期初三学段测评
数学试卷
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分.
整个试卷满分为120分.
一、选择题:(将唯一正确答案代号填在括号内.每小题2分,满分30分)
1.下列方程中是一元二次方程的是 ( )
A. B.
B.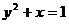 C.
C. D.
D.
2.下列命题中的真命题是 ( )
A.三个角对应相等的两个三角形全等
B.三条边对应相等的两个三角形全等
C.面积相等的两个三角形全等
D.周长相等的两个三角形全等
3.一元二次方程 的根的情况是 ( )
的根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
4.下列三角形:①有两个角均为60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰的高的等腰三角形.其中是等边三角形的有 ( )
A.①②③ B.①②④ C.①③ D.①②③④
5.方程 的解是 ( )
的解是 ( )
A. B.
B. C.
C.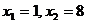 D.
D.
6.下列说法正确的是 ( )
A.所有的命题都有逆命题
B.所有的定理都有逆定理
C.若原命题是真命题,则其逆命题也是真命题
D.命题都可以看作是定理
7.若分式 的值是零,则
的值是零,则 的值是 ( )
的值是 ( )
A.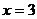 B.
B. C.
C. 或
或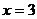 D.
D.
8.到△ABC的三个顶点距离相等的点是△ABC的 ( )
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点
D.三边垂直平分线的交点
9.以3和-1为根的一元二次方程是 ( )
A. B.
B.
C. D.
D.
10.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是 ( )
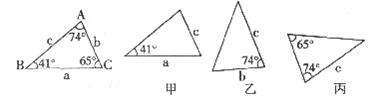
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
11.若实数 ,
, 满足
满足 ,则
,则 的值为 ( )
的值为 ( )
A.-1或-2 B.-1或
12.如图,CD是Rt△ABC斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是 ( )

A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF
13.一元二次方程 的两个根的倒数和等于
( )
的两个根的倒数和等于
( )
A.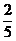 B.
B. C.
C. D.
D.
14.如图,P、Q分别是△ABC边上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若PB=PQ,PR=PS.则下列结论:①AS=AR;②△BRP≌△QSP;③AQ+AB=2AR.其中正确的有 ( )
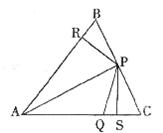
A.0个 B.1个 C.2个 D.3个
15.一个美术兴趣小组在新年来临之际互送自制贺卡一张,已知全组共互送贺卡20张,则这个小组有 ( )
A.4人 B.5人 C.8人 D.10人
二、填空题:(将正确答案填在横线上.每小题3分,满分30分)
16.方程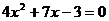 的二次项是
,一次项系数是 ,常数项是 .
的二次项是
,一次项系数是 ,常数项是 .
17.在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于点D,垂足为E,则∠DBC的度数是
18.已知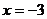 是方程
是方程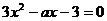 的一个根,则a=
的一个根,则a=
19.如图,点A、B分别在∠COD的边上,AD与BC相交于点E,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=

20.请你写一个两根互为相反数的一元二次方程
21.在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,若DC=
22.已知方程 有两个相等的实数根,则k=
有两个相等的实数根,则k=
23.已知AD是等边△ABC的高,BE是AC边的中线,AD与BE交于点F.则∠AFE的度数为
24.某粮店第二月份的销售量比第一月份的销售量增长了 %,第三月份的销售量又比第二月份的销售量增长了
%,第三月份的销售量又比第二月份的销售量增长了 %,第三月份的销售量比第一月份的销售量增长了44%,则
%,第三月份的销售量比第一月份的销售量增长了44%,则 %=
.
%=
.
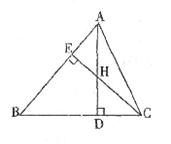
25.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE相交于点H,请你填写一个适当的条件,使△AEH≌△CEB.你所填的条件是
三、解方程:(每小题5分,满分10分)
26. .
.
27. .
.
四、解答题:(每小题6分,满分18分)
28.已知:关于 的方程
的方程 .
.
(1)当m取何值时,方程有两个实数根.
(2)请给m选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个根.
29.将一条长为
30.如图,D是△ABC的边AB上的一点,E是AC的中点,过点C作AB的平行线交DE的延长线于点F.
(1)求证:△ADE≌△CFE;
(2)若AB=9,FC=7,求BD的长.

五、实际应用题:(满分9分)
31.春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:

某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少名员工去天水湾风景区旅游?
六、探索与创新题:(第32小题6分,第33小题12分,满分18分)
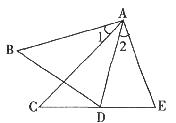
32.如图,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.请你以其中三个作为条件,余下的一个作为结论,编一道数学题,并写出解答过程.(要求写出已知,求证及证明过程)
33.如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
(4)归纳(1),(2),(3),请用简捷的语言表述BD与DE,CE的关系.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com