
2008-2009学年度聊城市临清第一学期九年级学业水平测试
数学试卷
第Ⅰ卷(选择题,共36分)
一、单项选择题(本题共l2个小题。每小题3分,共36分)
1.下列计算正确的是
A.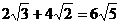 B.
B.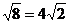
C.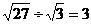 D.
D.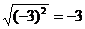
2.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为
A.1 B.-l C.l或-l D.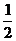
3.已知Rt△ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是
A.m?sin40° B.m?cos40°
C.m?tan40°
D.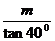
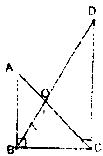
4.将一副三角板按下图所示叠放,则△AOB与△DOC的面积之比等于
A.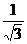 B.
B.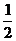 C.
C. D.
D.
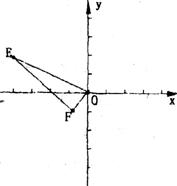
5.已知:如下图,点E(-4,2),点F(-1,-1),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E /的坐标为
A.(2,-l)或(-2,1) B.(8,-4)或(-8,1)
C.(2,-l) D.(8,-4)
6.方程(x+1)(x-3)=5的解是
A.xl =1,x2 =-3 B.xl =4,x2 =-
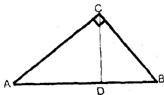
7.如下图:在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC= ,BC=2,那么sin∠ACD=
,BC=2,那么sin∠ACD=
A.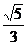 B.
B.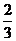 C.
C. D.
D.
8.如下图,在平地上种植树时,要求株距(相邻两树间的水平距离)为
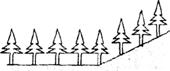
A.
9.在李咏主持的“幸远
A. B.
B.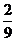 D.
D.  D.
D.
10.如下图,CD是平面镜,光线从A点射出。经CD上点E反射后照射到B点,若入射角为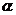 (入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan
(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan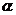 的值为
的值为
A. B.
B. C.
C. D.
D.
11.据
A.12% B.16% C.20% D.25%
12.二次函数y=ax2+bx+c的图像如下图所示,则下列关系不正确的是

A.a<0 B.abc>
第Ⅱ卷 (非选择题,共84分)
三、填空题(本题共5个小题.每小题3分。共l5分)
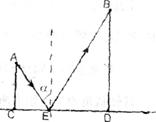
13.若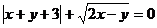 ,则
,则 ___________。
___________。
14.如下图,∠ACB=∠ADC=90°,AC= ,AD=2,则当AB=__________时,这两个直角三角形相似。
,AD=2,则当AB=__________时,这两个直角三角形相似。

15.经过某十字路口的汽车,它可继续直行,也可向左转或向右转,如果这三种可能性大小相同。那么两辆汽车经过这个十字路口,至少有一辆车向左转的概率为_______________。
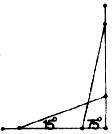
16.如下图。小明发现在教学楼走廊上有一拖把以l5°的倾斜角靠在栏杆上。严重影响了同学们的行走安全。他自觉地将拖把挪动位置,使其倾斜角为750,如果拖把的总长为1.80米,则小明拓宽了行路通道__________米(结果保留三个有效数字)。
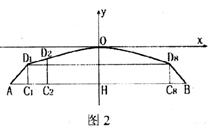
17.“中山桥”是位于兰州市中心、横跨黄河之上的一座百年老桥,如下图1,桥上有五个拱形桥架紧密相连,每个桥架的内部有一个水平横梁和八个垂直于横梁的立柱,气势雄伟,素有“天下黄河第一桥”之称.如下图2,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线DlOD8组成.若建立如图所示的直角坐标系。跨度AB=44米,∠A=45°,ACl=4,点D2的坐标为(-13,-l.69),则桥架的拱高OH=_______________米.

四、解答题(本题共8个小题。共66分,解答应写出必要的文字说明、证明过程或推演步骤)
18.(本题满分5分)解方程:2x2-5x+1=0(用配方法)。
19.(本题满分6分)
如下图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。

(1)填空:∠ABC=__________,BC=_____________;
(2)请判断△ABC和△DEF是否相似,并证明你的结论。
20.(本题满分8分)
如下图,路灯(P点)距地面8米,身高l.6米的小明从距路灯的底部(0点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?

21.(本题满分8分)
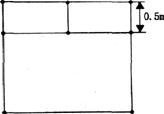
在高度为2.8m的一面墙上,准备开凿一个矩形窗户。先用9.5m长的铝合金条制成如下图所示的窗框。问:窗户的宽和高各是多少米,其透光面积为3m2(铝合金条的宽度忽略不计)?
22.(本题满分7分)
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据下图中数据计算回答:

小敏身高l.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
23.(本题满分l0分)
小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏。他们用四种字母做成十枚棋子,其中A棋一枚,B棋两枚,C棋三枚,D棋四枚。“字母棋”的游戏规则为:
①游戏时两人各摸一枚进行比赛称一轮比赛,先摸者摸出的棋不放回;
②A棋胜B棋、C棋;B棋胜C棋、D棋;C棋胜D棋;
③相同棋子不分胜负。
(1)若小玲先摸,问小玲摸到C棋的概率是多少?
(2)已知小玲先摸到C棋,小军在剩余的9枚棋中随机摸一枚,问这一轮中小玲胜小军的概率是多少?
(3)已知小玲先摸一枚棋,小军在剩余的9枚棋中随机摸一枚,问这一轮中小玲摸到哪种棋胜小军的概率最大?
24.(本题满分l0分)
如下图, ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A和B.
ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A和B.

(1)求点A、B、C的坐标;
(2)若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式。
25.(本题满分l2分)
如下图,在Rt△ABC中。∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度。过点D作DE∥BC交于点E,设动点D运动的时间为x秒,AE的长为y.
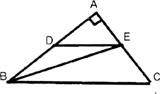
(1)求y关于x的函数关系式,并写出自变量的取值范围;
(2)当x为何值时,△BDE的面积S有最大值,最大值为多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com