
2008-2009学年度北京市崇文区第二学期初三统一练习(一)
数学试卷
一、选择题(共8道小题,每小题4分,共32分)
1. 的相反数是
的相反数是
A. B.
B. 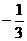 C.
C.  D. 3
D. 3
2.根据北京移动公布的短信发送量显示,从大年三十到初六,7天内北京移动手机用户彩信发送总量超过了67,000,000条.将67000000用科学记数法表示应为
A.67 B.
B.  C.6.7
C.6.7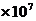 D.6.7
D.6.7
3.为了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班9名学生进行了调查,有关数据如下表:
每周做家务的时间(小时)
0
1
2
3
4
人数(人)
2
2
3
1
1
则这9名学生每周做家务劳动的时间的众数及中位数分别是
A.3,2.5 B.1,2 C.3,3 D.2,2
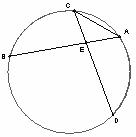
4.如图,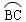 与
与 的度数相等,弦AB与弦CD交于点E,
的度数相等,弦AB与弦CD交于点E, ,则
,则 等于
等于
A. B.
B. C.
C.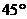 D.
D.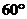
5.若一个多边形的内角和等于它的外角和,则这个多边形的边数是
A.4 B.5 C.6 D. 7
6.若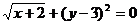 .则
.则 的值为
的值为
A.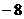 B.8 C.
9 D.
B.8 C.
9 D.
7.一布袋中有红球8个,白球5个和黑球12个,它们除颜色外没有其他区别,随机地从袋中取出1球是黑球的概率为( )
A. B. C. D.
8.下图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是
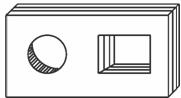

二、填空题(共4道小题,每小题4分,共16分)
9.在函数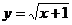 中,自变量
中,自变量 的取值范围是
.
的取值范围是
.
10.分解因式: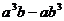 =
.
=
.
11.如图,在△ 中,
中, ,
, ,
,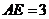 ,
, ,则
,则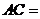 .
.

12.一组按规律排列的数:2,0,4,0,6,0,…,其中第7个数是
,第 个数是
(
个数是
( 为正整数).
为正整数).
三、解答题(共5道小题,共25分)
13.(本小题满分5分)
计算:
 +
+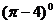
 .
.
14.(本小题满分5分)
解不等式组: 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
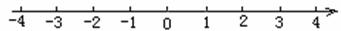
15.(本小题满分5分)
如下图,已知 .求证:
.求证: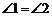 .
.

16.(本小题满分5分)
某公司市场营销部的营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示。根据图象提供的信息,解答下列问题:

(I)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
(II)已知该公司某营销员5月份的销售量为1.2万件,求该营销员5月份的收入.
17.(本小题满分5分)
已知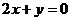 ,求
,求 的值.
的值.
四、解答题(共2道小题,共10分)
18.(本小题满分5分)
如图,以等腰 中的腰
中的腰 为直径作⊙
为直径作⊙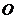 ,交底边
,交底边 于点
于点 .过点
.过点 作
作 ,垂足为
,垂足为 .
.

(I)求证: 为⊙
为⊙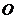 的切线;
的切线;
(II)若⊙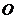 的半径为5,
的半径为5,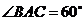 ,求
,求 的长.
的长.
19.(本小题满分5分)
如图,在梯形ABCD中,AD∥BC, .若AC⊥BD,AD+BC=
.若AC⊥BD,AD+BC=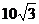 , 且
, 且 , 求CD的长.
, 求CD的长.

五、解答题(共3道小题,共15分)
20.(本小题满分5分)
九年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为100分)进行了一次初步统计,80分以上(含80分)有17人,但没有满分,也没有低于30分的.为更清楚了解本班的考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示.请根据图中提供的信息回答下列问题:
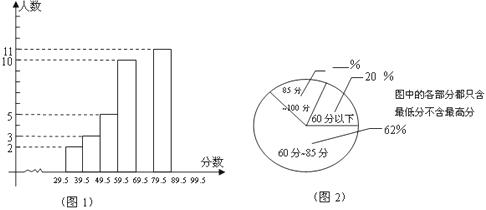
(I)该班60分以下(不含60分)的有 人;
(II)该班共有 名学生参加了考试;
(III)补全两个图中三个空缺的部分.
21.(本小题满分5分)
将进价为40元的商品按50元售出时,能卖出500个,经市场调查得知,该商品每涨价1元,其销售量就减少10个,为了赚取8000元的利润,售价应定为多少元?
22.(本小题满分5分)
如下图,矩形纸片ABCD中, 厘米,
厘米, 厘米,点E在AD上,且AE=6厘米,点P是AB边上一动点.按如下操作:
厘米,点E在AD上,且AE=6厘米,点P是AB边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点E重合,展开纸片得折痕MN(如图①);
步骤二,过点P作 ,交MN所在的直线于点Q,连结QE(如图②).
,交MN所在的直线于点Q,连结QE(如图②).

(I)无论点P在AB边上任何位置,都有PQ QE(填“>”、“=”、“<”);
(II)如图③所示,将矩形纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
(i)当点P在A点时,PT与MN交于点 ,
, 点的坐标是(
, );
点的坐标是(
, );
(ii)当PA=6厘米时,PT与MN交于点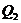 ,
,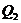 点的坐标是(
, );
点的坐标是(
, );
(iii)当PA= 厘米时,在图③中用尺规作出MN(不要求写作法,要求保留作图痕迹),PT与MN交于点
厘米时,在图③中用尺规作出MN(不要求写作法,要求保留作图痕迹),PT与MN交于点 ,
, 点的坐标是(
,
).
点的坐标是(
,
).

六、解答题(共3道小题,共22分)
23.(本小题满分7分)
已知:关于x的一元二次方程kx2+(2k-3)x+k-3 = 0有两个不相等实数根(k<0).
(I)用含k的式子表示方程的两实数根;
(II)设方程的两实数根分别是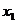 ,
, (其中
(其中 ),若一次函数y=(3k-1)x+b与反比例函数y =
),若一次函数y=(3k-1)x+b与反比例函数y = 的图像都经过点(x1,kx2),求一次函数与反比例函数的解析式.
的图像都经过点(x1,kx2),求一次函数与反比例函数的解析式.
24.(本小题满分7分)
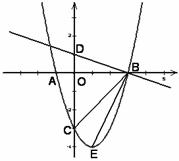
如图,抛物线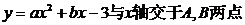 ,与
,与 轴交于点
轴交于点 ,且
,且 .
.
(I)求抛物线的解析式;
(II)探究坐标轴上是否存在点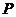 ,使得以点
,使得以点 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?
若存在,求出 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;
(III)直线 交
交 轴于
轴于 点,
点, 为抛物线顶点.若
为抛物线顶点.若 ,
, 的值.
的值.
25.(本小题满分8分)
在等边 的两边AB、AC所在直线上分别有两点M、N,D为
的两边AB、AC所在直线上分别有两点M、N,D为 外一点,且
外一点,且 ,
, ,BD=DC. 探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及
,BD=DC. 探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及 的周长Q与等边
的周长Q与等边 的周长L的关系.
的周长L的关系.

(I)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是
; 此时 ;
;
(II)如图2,点M、N边AB、AC上,且当DM DN时,猜想(I)问的两个结论还成立吗?写出你的猜想并加以证明;
DN时,猜想(I)问的两个结论还成立吗?写出你的猜想并加以证明;
(III) 如图3,当M、N分别在边AB、CA的延长线上时,若AN= ,则Q=
(用
,则Q=
(用 、L表示).
、L表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com