1．|－9|的平方根是

A．81．                B．±3．            C．3．              D．－3．

2．计算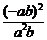的结果是

A．a．                 B．b．              C．1．              D．－b．

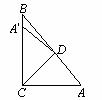
3．如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=

A．40°．              B．30°．           C．20°．           D．10°．

4．从只装有4个红球的袋中随机摸出一球，若摸到白球的概率是p₁，摸到红球的概率是p₂，则

A．p₁=1，p₂=1．   B．p₁=0，p₂=1．  C．p₁=0，p₂=．    D．p₁=p₂=．

5．若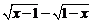=（x＋y）²，则x－y的值为

A．－1．              B．1．               C．2．                    D．3．

6．等腰梯形ABCD中，E、F、G、H分别是各边的中点，则四边形EFGH的形状是

A．平行四边形．  B．矩形．           C．菱形．               D．正方形．

7．关于x的方程ax²－（a＋2）x＋2=0只有一解（相同解算一解），则a的值为

A．a=0．              B．a=2．           C．a=1．                D．a=0或a=2．

8．函数y=ax＋1与y=ax²＋bx＋1（a≠0）的图象可能是

9．长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是

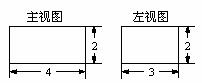
A．12cm²．          B．8cm²．         C．6cm²．                D．4cm²．

10．若不等式组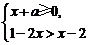有解，则a的取值范围是

A．a＞－1．         B．a≥－1．       C．a≤1．                 D．a＜1．

11．=______．

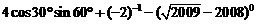12．定义a※b=a²－b，则（1※2）※3=______．

13．将点P向左平移2个单位，再向上平移1个单位得到P′（－1，3），则点P的坐标是______．

14．函数y=（x－2）（3－x）取得最大值时，x=______．

15．如图，Rt△ABC中，∠C=90°，AC=6，BC=8．则△ABC的内切圆半径r=______．

16．从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是______．

17．直线y=ax（a＞0）与双曲线y=交于A（x₁，y₁）、B（x₂，y₂）两点，则4x₁y₂－3x₂y₁=______．

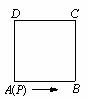
18．如图，正方形ABCD边长为1，动点P从A点出发，沿正方形的边按逆时针方向运动，当它的运动路程为2009时，点P所在位置为______；当点P所在位置为D点时，点P的运动路程为______（用含自然数n的式子表示）．

19．（本题满分6分）已知x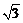=2＋，y=2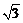－，计算代数式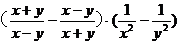的值．

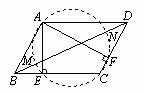
20．（本题满分8分）如图，在□ABCD中，∠BAD为钝角，且AE⊥BC，AF⊥CD．

（1）求证：A、E、C、F四点共圆；

（2）设线段BD与（1）中的圆交于M、N．求证：BM=ND．

21．（本题满分10分）星期天，小明和七名同学共8人去郊游，途中，他用20元钱去买饮料，商店只有可乐和奶茶，已知可乐2元一杯，奶茶3元一杯，如果20元钱刚好用完．

（1）有几种购买方式？每种方式可乐和奶茶各多少杯？

（2）每人至少一杯饮料且奶茶至少二杯时，有几种购买方式？

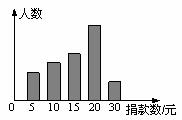
22．（本题满分10分）某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，下图是根据这组数据绘制的统计图，图中从左到右各长方形高度之比为3∶4∶5∶8∶2，又知此次调查中捐15元和20元的人数共39人．

（1）他们一共抽查了多少人？捐款数不少于20元的概率是多少？

（2）这组数据的众数、中位数各是多少？

（3）若该校共有2310名学生，请估算全校学生共捐款多少元？

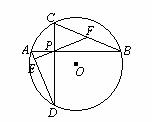
23．（本题满分10分）如图，半径为2的⊙O内有互相垂直的两条弦AB、CD相交于P点．

（1）求证：PA?PB=PC?PD；

（2）设BC的中点为F，连结FP并延长交AD于E，求证：EF⊥AD：

（3）若AB=8，CD=6，求OP的长．

24．（本题满分10分）一次函数y=kx＋b的图象与x、y轴分别交于点A（2，0），

B（0，4）．

（1）求该函数的解析式；

（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点的坐标．

25．（本题满分12分）一开口向上的抛物线与x轴交于A（m－2，0），B（m＋2，0）两点，记抛物线顶点为C，且AC⊥BC．

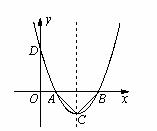
（1）若m为常数，求抛物线的解析式；

（2）若m为小于0的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点？

（3）设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．