1．2的相反数是  （    ）

A．2                             B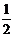．-2                          C．                          D．

2．cos60°的值等于（    ）

A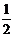．                        B．                       C．                       D．

3．数据1，0，4，3的平均数是（    ）

A．3                          B．2．5                   C．2                         D．1．5

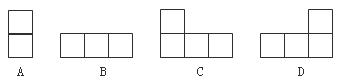
4．下图中几何体的主视图是 （    ）

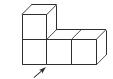
正面

5．已知图中的两个三角形全等，则∠的度数是（    ）

A．72°                          B．60°                        C．58°                        D．50°

6．如图，DE是△ABC关的中位线，若BC的长为3cm，则DE的长是（    ）

A．2cm                      B．1．5cm                  C．1．2cm                  D．1cm

7．当x=-2时，代数式x+1的值是（    ）

A．-1                            B．-3                          C．1                            D．3

8．式子在实数范围内有意义，则x的取值范围是（    ）

   A．x≥1                         B．x＞1                     C．x≤1                       D．x≠1

9．在下列各式中，与（a-b）²一定相等的是（    ）

   A．a²+2ab+b²                B．a²-b²                 C．a²+b²                       D．a²-2ab+b²

10 如图，AB是⊙O的直径，C是⊙O上一点，且∠A=45°，则下列结论中正确的是（    ）

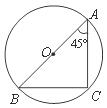
A．BC=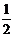AB            B．BC=AC                  C．BC＜AC              D．BC＞AC

11．方程x（x+1）=0的解是（    ）

A．x=0                        B．x=-1                       C．x₁=0, x₂=-1             D．x₁=0, x₂=1

12．一次函数y=-x+2的图象是（    ）

13．计算：3a-2a=            ．

14．在反比例函数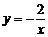中，当y=1时，x=           ．

15．100件产品中仅有4件是次品，从中随机抽出1件，则抽到次品的概率是       ．

16．“a的2倍与1的和”用代数式表示是                       ．

17．如图，菱形ABCD中，∠B=60°，AB=5，则AC=        ．

18．如图，将矩形纸片ABCD沿EF折叠后，点C、D分别落在点C′、D′处，若∠AFE=65°，则∠C′EF=           度． 

19．（满分8分，每小题4分）

（1）计算：；（2）化简：（a+1）（a-1）-a（a-1）．

20．（满分8分）目前我省小学和初中在校生共136万人，其中小学在校生人数比初中在校生人数的2倍少2万人． 问目前我省小学和初中在校生各有多少万人？

21．（满分8分）根据图1、图2所提供的信息，解答下列问题：

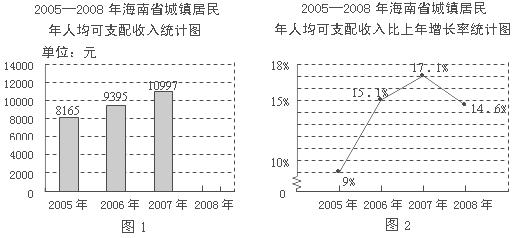
（1）2007年海南省城镇居民人均可支配收入为       元，比2006年增长       %；

（2）求2008年海南省城镇居民人均可支配收入（精确到1元），并补全条形统计图；

（3）根据图1指出：2005―2008年海南省城镇居民人均可支配收入逐年        

（填“增加”或“减少”）．

22．（满分8分）如图所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：

（1）分别写出点A、B两点的坐标；

（2）作出△ABC关于坐标原点成中心对称的△A₁B₁C₁；

（3）作出点C关于是x轴的对称点P． 若点P向右平移x个单位长度后落在△A₁B₁C₁的内部，请直接写出x的取值范围．

23．（满分11分）如图1,在△ABC中，∠ACB=90°，∠CAB=30°, △ABD是等边三角形，E是AB的中点，连结CE并延长交AD于F．

（1）求证：① △AEF≌△BEC；② 四边形BCFD是平行四边形；

（2）如图2，将四边形ACBD折叠,使D与C重合，HK为折痕，求sin∠ACH的值．

24．（满分13分）如图1，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为 （2,4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．

（1）求该抛物线所对应的函数关系式；

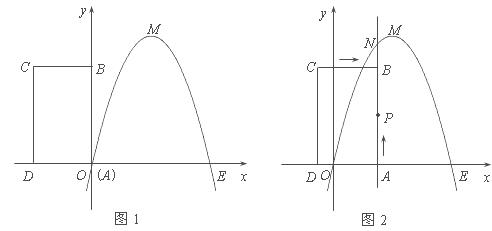
（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．

① 当t=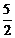时，判断点P是否在直线ME上，并说明理由；

② 设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．