1．?5的相反数是 （    ）

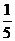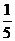       A．              B．?                       C．?5             D．5

2．不等式?2x<4的解集是     （    ）                 

       A．x>?2           B．x<?2                C．x>2             D．x<2

3．下列调查适合普查的是    （    ）                    

       A．调查2009年6月份市场上某品牌饮料的质量

       B．了解中央电视台直播北京奥运会开幕式的全国收视率情况

       C． 环保部门调查5月份黄河某段水域的水质量情况

       D．了解全班同学本周末参加社区活动的时间

4．方程=x的解是      （    ）

       A．x=1                                            B．x=0

       C．x₁=1   x₂=0                                 D．x₁=?1   x₂=0   

5．如图所示，在平面直角坐标系中，点A、B的坐标分别为（?2，0）和（2，0）．月牙①绕点B顺时针旋转90⁰得到月牙②，则点A的对应点A’的坐标为   （    ）

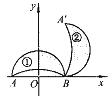
       A．（2，2）         B．（2，4）          C．（4，2）          D．（1，2）

6．一个几何体由一些大小相同的小正方体组成，如图是它的主视图和俯视图，那么组成该几何体所需小正方体的个数最少为      （    ）

       A．3                     B． 4                     C．  5                 D．6

7．16的平方根是             ．

8．如图，AB//CD,CE平分∠ACD，若∠1=25⁰，那么∠2的度数是               ．

9．下图是一个简单的运算程序．若输入X的值为?2,则输出的数值为               ．

10．如图,在ABCD中，AC与BD交于点O，点E是BC边的中点，OE=1,则AB的长是         ．

11．如图，AB为半圆O的直径，延长AB到点P，使BP=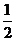AB，PC切半圆O于点C，点D是上和点C不重合的一点，则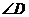的度数为               ．

12．点A（2，1）在反比例函数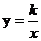的图像上，当1?x?4时，y的取值范围是          ．

13．在一个不透明的袋子中有2个黑球、3个白球，它们除颜色外其他均相同．充分摇匀后,先摸出1个球不放回,再摸出1个球,那么两个球都是黑球的概率为                  ．

14．动手操作：在矩形纸片ABCD中，AB=3,AD=5．如图所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为       ．

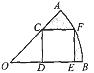
15．如图，在半径为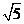，圆心角等于45⁰的扇形AOB内部作一个正方形CDEF，使点C在OA上，点D、E在OB上，点F在上，则阴影部分的面积为（结果保留）               ．

16．（8分）先化简，然后从中选取一个你认为合适的数作为x的值代入求值．

17．（9分）如图所示，∠BAC=∠ABD,AC=BD，点O是AD、BC的交点，点E是AB的中点．试判断OE和AB的位置关系,并给出证明．

18．（9分）2008年北京奥运会后，同学们参与体育锻炼的热情高涨．为了解他们平均每周的锻炼时间，小明同学在校内随机调查了50名同学，统计并制作了如下的频数分布表和扇形统计图．

  根据上述信息解答下列问题：

    （1）m=______，n=_________；

    （2）在扇形统计图中，D组所占圆心角的度数为_____________；

    （3）全校共有3000名学生，估计该校平均每周体育锻炼时间不少于6小时的学生约有

  多少名?

l9．（9分）暑假期间，小明和父母一起开车到距家200千米的景点旅游．出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升．

    （1）已知油箱内余油量y（升）是行驶路程x（千米）的一次函数，求y与x的函数关系式；

    （2）当油箱中余油量少于3升时，汽车将自动报警．如果往返途中不加油，他们能否在汽车报警前回到家?请说明理由．

20．（9分）如图所示，电工李师傅借助梯子安装天花板上距地面2 ．90m的顶灯．已知梯子由两个相同的矩形面组成，每个矩形面的长都被六条踏板七等分，使用时梯脚的固定跨度为1m．矩形面与地面所成的角α为78°．李师傅的身高为l．78m，当他攀升到头顶距天花板0．05～0．20m时，安装起来比较方便．他现在竖直站立在梯子的第三级踏板上，请你通过计算判断他安装是否比较方便?

    （参考数据：sin78°≈0．98，cos78°≈0．21，tan78°≈4．70．）

21． （10分）如图，在Rt△ABC中，∠ACB=90°, ∠B =60°，BC=2。点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE∥AB交直线l于点E，设直线l的旋转角为α．

    （1）①当α=________度时，四边形EDBC是等腰梯形，此时AD的长为_________；

         ②当α=________度时，四边形EDBC是直角梯形，此时AD的长为_________；

    （2）当α=90°时,判断四边形EDBC是否为菱形，并说明理由．

22． （10分）某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共l5台．三种家电的进价和售价如下表所示：

 （1）在不超出现有资金的前提下，若购进电视机的数量和冰箱的数量相同，洗衣机数量不大于电视机数量的一半，商场有哪几种进货方案?

    （2）国家规定：农民购买家电后，可根据商场售价的13％领取补贴．在（1）的条件下．如果这15台家电全部销售给农民，国家财政最多需补贴农民多少元?

23．（11分）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）．抛物线y=ax²+bx过A、C两点．   

（1）直接写出点A的坐标，并求出抛物线的解析式；

    （2）动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD

向终点D运动．速度均为每秒1个单位长度，运动时间为t秒．过点P作PE⊥AB交AC于点E

    ①过点E作EF⊥AD于点F，交抛物线于点G．当t为何值时，线段EG最长?

②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?

请直接写出相应的t值．