
2009年福建省泉州市丰泽区初中学业质量检查
数学试卷
(满分:150分;考试时间:120分钟)
一、选择题(每小题4分,共24分)
1. 的相反数是( )
的相反数是( )
A. 8
B.  C.
C. 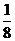 D.
D. 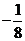
2.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,6.5,9.1,7.7,则这四人中,射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
3.如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为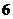 的面是底面,则朝上一面所标注的数字为( )
的面是底面,则朝上一面所标注的数字为( )
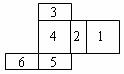
A.5 B.
4.下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )
A.①②③ B.①② C.①③ D.②③
5.不等式组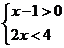 的解是( )
的解是( )
A.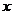 >1 B.
>1 B.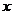 <2 C.1<
<2 C.1<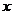 <2 D.无解
<2 D.无解
6.如下图,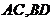 是⊙
是⊙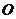 直径,且
直径,且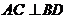 ,动点
,动点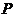 从圆心
从圆心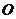 出发,沿
出发,沿 路线作匀速运动,设运动时间为
路线作匀速运动,设运动时间为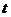 (秒),
(秒),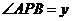 (度),则下列图象中表示
(度),则下列图象中表示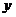 与
与 之间的函数关系最恰当的是( )
之间的函数关系最恰当的是( )
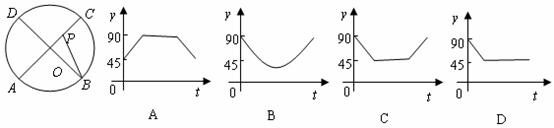
二、填空题(第小题3分,共36分)
7.计算: =_________________.
=_________________.
8.分解因式: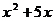 =_______________________.
=_______________________.
9.北京奥运会国家体育场“鸟巢”的建筑面积约为258000平方米,用科学记数法可表示约为 _________________平方米.
10.计算: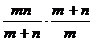 =___________.
=___________.
11.六边形的内角和等于________________度.
12.反比例函数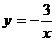 的图象在第二象限和第___________象限.
的图象在第二象限和第___________象限.
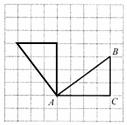
13.在下图方格纸中,把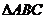 绕
绕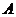 逆时针旋转_________度后可得
逆时针旋转_________度后可得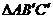 .
.
14.在一个不透明的摇奖箱内装有20个形状、大小、质地等完全相同的小球,其中只有5个球标有中奖标志,则随机抽取一个小球中奖的概率是___________.
15.某个圆锥的侧面展开图形是一个半径为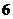
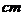 ,圆心角为
,圆心角为 的扇形,则这个圆锥的底面半径为______________
的扇形,则这个圆锥的底面半径为______________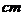 .
.
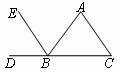
16.如下图,不添加辅助线,请写出一个能判定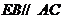 的条件:
.
的条件:
.
17.某工地实施爆破,操作人员点燃导火线后,必须在炸药爆炸前跑到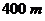 外安全区域,若导火线燃烧的速度为
外安全区域,若导火线燃烧的速度为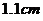 /秒,人跑步的速度为
/秒,人跑步的速度为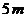 /秒,则导火线的长
/秒,则导火线的长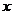 应满足的不等式是:
.
应满足的不等式是:
.
18.下面是一个三角形数阵: 1------------------------第1行
2 3 ------------------第2行
4 5 6------------------第3行
7 8 9 10------------第4行
……
根据该数阵的规律,第8行第2个数是 .
三、解答题(共90分)在答题卡上相应题目的答题区域内作答.
19.(8分)计算: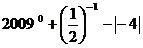
20.(8分)先化简下面代数式,再求值:
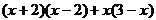 ,其中
,其中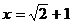 .
.
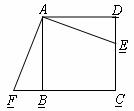
21.(8分)如下图,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F,求证:△ADE≌△ABF.
22.(8分)下边下面两图是根据某校初三(1)班同学的上学方式情况调查所制作的条形和扇形统计图,请你根据图中提供的信息,解答以下问题:
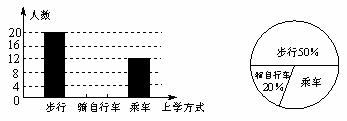
(1)求该班学生人数,并将条形统计图补充完整;
(2)若该校初三年有600名学生,试估计该年级乘车上学的人数。
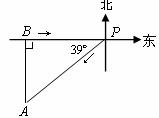
23.(8分)如下图,小岛 位于港口
位于港口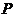 的西偏南
的西偏南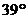 方向,小岛
方向,小岛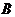 位于
位于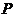 的正西方向,且位于
的正西方向,且位于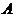 的正北方向,已知小岛
的正北方向,已知小岛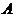 与港口
与港口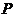 相距
相距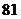 海里.
海里.
(1)求小岛 与港口
与港口 的距离(精确到
的距离(精确到 海里);
海里);
(2)甲船从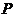 出发驶向
出发驶向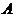 ,乙船从
,乙船从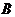 出发驶向
出发驶向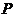 ,甲、乙两船的行驶速度分别为
,甲、乙两船的行驶速度分别为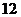 海里/小时和
海里/小时和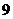 海里/小时.两船同时出发,问:几小时后,它们与
海里/小时.两船同时出发,问:几小时后,它们与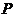 的距离相等?
的距离相等?
24.(8分)有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形(如下图).将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.

(1)求出两次摸牌的所有等可能结果(用树状图或列表法求解,纸牌可用A,B,C表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.
25.(8分)如下图,已知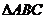 的面积为
的面积为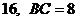 .现将
.现将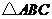 沿直线
沿直线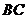 向右平移
向右平移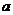 个单位到
个单位到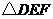 的位置.
的位置.

(1)当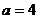 时,求
时,求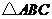 所扫过的面积;
所扫过的面积;
(2)连结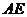 、
、 ,设
,设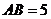 ,当
,当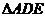 是以
是以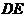 为一腰的等腰三角形时,求
为一腰的等腰三角形时,求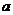 的值.
的值.
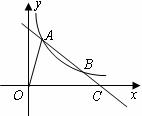
26.(8分) 如下图,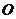 为坐标原点,点
为坐标原点,点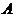
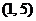 和点
和点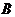
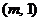 均在反比例函数
均在反比例函数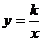 图象上.
图象上.
(1)求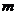 、
、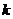 的值;
的值;
(2)设直线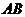 与
与 轴交于点
轴交于点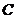 ,求
,求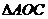 的面积.
的面积.
27.(13分)某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25?,设每双鞋的成本价为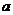 元.
元.
(1)试求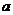 的值;
的值;
(2)为了扩大销售量,公司决定拿出一定量的资金做广告,根据市场调查,若每年投入广告费为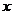 (万元)时,产品的年销售量将是原销售量的
(万元)时,产品的年销售量将是原销售量的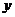 倍,且
倍,且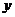 与
与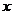 之间的关系如下图所示,可近似看作是抛物线的一部分.
之间的关系如下图所示,可近似看作是抛物线的一部分.
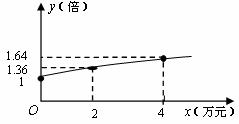
①根据图象提供的信息,求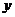 与
与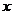 之间的函数关系式;
之间的函数关系式;
②求年利润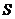 (万元)与广告费
(万元)与广告费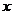 (万元)之间的函数关系式,并请回答广告费
(万元)之间的函数关系式,并请回答广告费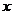 (万元)在什么范围内,公司获得的年利润
(万元)在什么范围内,公司获得的年利润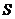 (万元)随广告费的增大而增多?
(万元)随广告费的增大而增多?
(注:年利润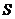 =年销售总额-成本费-广告费)
=年销售总额-成本费-广告费)
28.(13分)如下图,在平面直角坐标系中,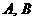 两点的坐标分别为
两点的坐标分别为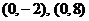 ,以
,以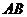 为一边作正方形
为一边作正方形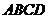 ,再以
,再以 为直径的半圆
为直径的半圆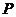 .设
.设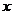 轴交半圆
轴交半圆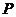 于点
于点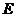 ,交边
,交边 于点
于点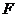 .
.
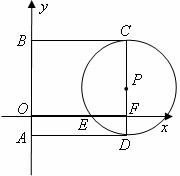
(1)求线段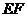 的长;
的长;
(2)连接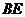 ,试判断直线
,试判断直线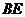 与⊙
与⊙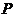 的位置关系,并说明你的理由;
的位置关系,并说明你的理由;
(3)直线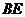 上是否存在着点
上是否存在着点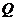 ,使得以
,使得以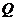 为圆心、
为圆心、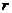 为半径的圆,既与
为半径的圆,既与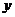 轴相切又与⊙
轴相切又与⊙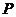 外切?若存在,试求
外切?若存在,试求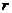 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
友情提示:①全卷得分低于90分,则本题得分计入总分,否则本题得分不计入总分;②计入后总分不得超过90分.
四、附加题(共10分)在答题卡上相应题目的答题区域内作答.
1.(5分)计算: =______________________.
=______________________.
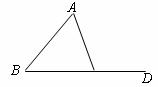
2.(5分)如下图,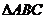 中,
中,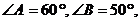 点
点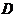 在的延长线上,则
在的延长线上,则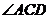 =___度.
=___度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com