
2009年黑龙江省齐齐哈尔市初中毕业学业考试
数学试卷
考生注意:
1.考试时间120分钟
2.全卷共三道大题,总分120分
一、单项选择题(每题3分,满分30分)
1.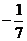 的绝对值是
的绝对值是
A.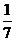 B.
B.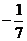 C.7 D.
C.7 D.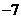
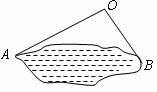
2.如图,为估计池塘岸边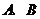 的距离,小方在池塘的一侧选取一点
的距离,小方在池塘的一侧选取一点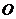 ,测得
,测得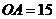 米,
米,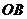 =
=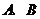 间的距离不可能是
间的距离不可能是
A.
3.下列运算正确的是
A.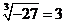 B.
B.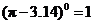 C.
C.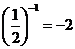 D.
D.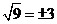
4.一组数据4,5,6,7,7,8的中位数和众数分别是( )
A.7,7 B.7,
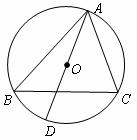
5.如图,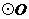 是
是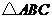 的外接圆,
的外接圆,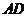 是
是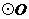 的直径,若
的直径,若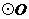 的半径为
的半径为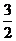 ,
, ,则
,则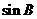 的值是(
)
的值是(
)
A.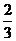 B.
B.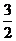 C.
C.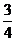 D.
D.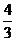
6.梯形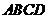 中,
中,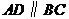 ,
,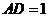 ,
,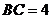 ,
, ,
,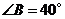 ,则
,则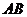 的长为(
)
的长为(
)
A.2 B.
7.一宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团20人准备同时租用这三种客房共7间,如果每个房间都住满,租房方案有( )
A.4种 B.3种 C.2种 D.1种
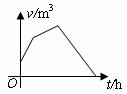
8.一个水池接有甲、乙、丙三个水管,先打开甲,一段时间后再打开乙,水池注满水后关闭甲,同时打开丙,直到水池中的水排空,水池中的水量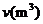 与时间
与时间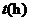 之间的函数关系如图,则关于三个水管每小时的水流量下列判断正确的是( )
之间的函数关系如图,则关于三个水管每小时的水流量下列判断正确的是( )
A.乙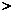 甲
B.丙
甲
B.丙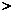 甲 C.甲
甲 C.甲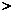 乙 D.丙
乙 D.丙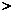 乙
乙
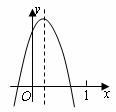
9.已知二次函数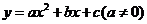 的图象如图所示,则下列结论:
的图象如图所示,则下列结论: ;
; 方程
方程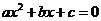 的两根之和大于0;
的两根之和大于0; 随
随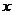 的增大而增大;④
的增大而增大;④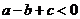 ,其中正确的个数( )
,其中正确的个数( )
A.4个 B.3个 C.2个 D.1个
10.在矩形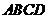 中,
中,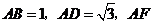 平分
平分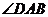 ,过
,过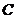 点作
点作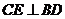 于
于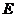 ,延长
,延长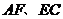 交于点
交于点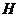 ,下列结论中:
,下列结论中: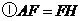 ;
;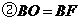 ;
; ;④
;④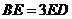 ,正确的是( )
,正确的是( )
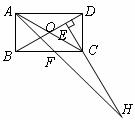
A.②③ B.③④ C.①②④ D.②③④
二、填空题(每题3分,满分30分)
11.中国齐齐哈尔SOS儿童村座落在齐齐哈尔市区西部,建成于1992年3月,是由国际SOS儿童村资助,以家庭形式收养、教育孤儿的社会福利事业单位,占地面积为37000平方米,这个数用科学记数法表示为___________平方米.
12.函数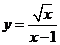 中,自变量
中,自变量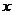 的取值范围是_____________.
的取值范围是_____________.
13.在英语句子“Wish you success!”(祝你成功!)中任选一个字母,这个字母为“s”的概率是____________.
14.反比例函数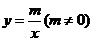 与一次函数
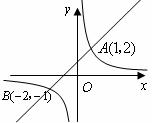
与一次函数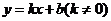 的图象如下图所示,请写出一条正确的结论:______________.
的图象如下图所示,请写出一条正确的结论:______________.
15.已知相交两圆的半径分别为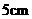 和
和 ,公共弦长为
,公共弦长为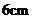 ,则这两个圆的圆心距是______________.
,则这两个圆的圆心距是______________.
16.当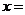 _____________时,二次函数
_____________时,二次函数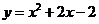 有最小值.
有最小值.
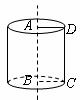
17.如下图,正方形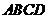 的边长为
的边长为 ,以直线
,以直线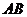 为轴,将正方形旋转一周,所得几何体的主视图的面积是_____________.
为轴,将正方形旋转一周,所得几何体的主视图的面积是_____________.
18.已知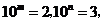 则
则 ____________.
____________.
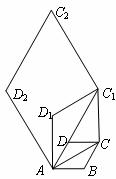
19.如下图,边长为1的菱形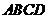 中,
中,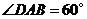 .连结对角线
.连结对角线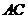 ,以
,以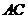 为边作第二个菱形
为边作第二个菱形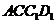 ,使
,使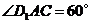 ;连结
;连结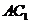 ,再以
,再以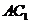 为边作第三个菱形
为边作第三个菱形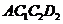 ,使
,使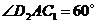 ;……,按此规律所作的第
;……,按此规律所作的第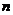 个菱形的边长为___________.
个菱形的边长为___________.
20.用直角边分别为3和4的两个直角三角形拼成凸四边形,所得的四边形的周长是____________.
三、解答题(满分60分)
21.(本小题满分5分)
先化简: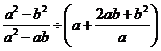 ,当
,当 时,请你为
时,请你为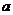 任选一个适当的数代入求值.
任选一个适当的数代入求值.
22.(本小题满分6分)
如下图,在平面直角坐标系中,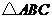 的顶点坐标为
的顶点坐标为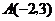 、
、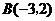 、
、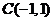 .
.
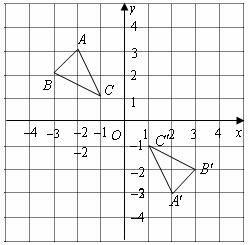
(1)若将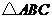 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的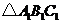 ;
;
(2)画出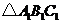 绕原点旋转
绕原点旋转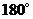 后得到的
后得到的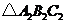 ;
;
(3) 与
与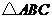 是中心对称图形,请写出对称中心的坐标:___________;
是中心对称图形,请写出对称中心的坐标:___________;
(4)顺次连结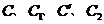 ,所得到的图形是轴对称图形吗?
,所得到的图形是轴对称图形吗?
23.(本小题满分6分)
在直角边分别为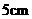 和
和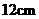 的直角三角形中作菱形,使菱形的一个内角恰好是三角形的一个角,其余顶点都在三角形的边上,求所作菱形的边长.
的直角三角形中作菱形,使菱形的一个内角恰好是三角形的一个角,其余顶点都在三角形的边上,求所作菱形的边长.
24.(本小题满分7分)
为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、成年人、青少年各年龄段实际人口的比例3∶5∶2,随机抽取一定数量的观众进行调查,得到如下统计图.

(1)上面所用的调查方法是_________(填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值;
A:_____________;B:_____________;
(3)求该地区喜爱娱乐类节目的成年人的人数.
25.(本小题满分8分)
邮递员小王从县城出发,骑自行车到A村投递,途中遇到县城中学的学生李明从A村步行返校.小王在A村完成投递工作后,返回县城途中又遇到李明,便用自行车载上李明,一起到达县城,结果小王比预计时间晚到1分钟。二人与县城间的距离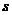 (千米)和小王从县城出发后所用的时间
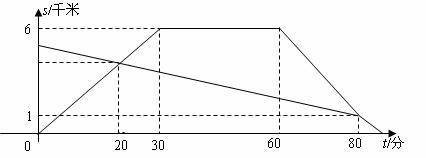
(千米)和小王从县城出发后所用的时间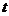 (分)之间的函数关系如图,假设二人之间交流的时间忽略不计.
(分)之间的函数关系如图,假设二人之间交流的时间忽略不计.
(1)小王和李明第一次相遇时,距县城多少千米?请直接写出答案.
(2)求小王从县城出发到返回县城所用的时间.
(3)李明从A村到县城共用多少时间?
26.(本小题满分8分)
如图1,在四边形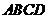 中,
中,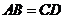 ,
,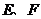 分别是
分别是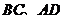 的中点,连结
的中点,连结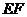 并延长,分别与
并延长,分别与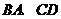 的延长线交于点
的延长线交于点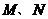 ,则
,则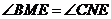 (不需证明).
(不需证明).
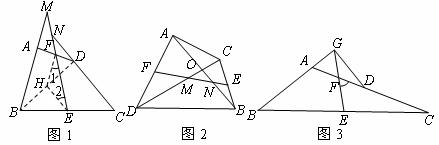
(温馨提示:在图1中,连结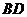 ,取
,取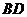 的中点
的中点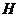 ,连结
,连结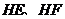 ,根据三角形中位线定理,证明
,根据三角形中位线定理,证明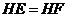 ,从而
,从而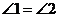 ,再利用平行线性质,可证得
,再利用平行线性质,可证得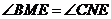 .)
.)
问题一:如图2,在四边形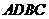 中,
中,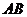 与
与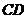 相交于点
相交于点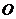 ,
,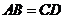 ,
,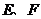 分别是
分别是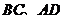 的中点,连结
的中点,连结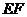 ,分别交
,分别交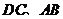 于点
于点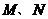 ,判断
,判断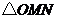 的形状,请直接写出结论.
的形状,请直接写出结论.
问题二:如图3,在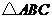 中,
中,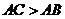 ,
,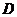 点在
点在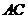 上,
上,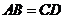 ,
,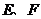 分别是
分别是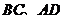 的中点,连结
的中点,连结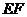 并延长,与
并延长,与 的延长线交于点
的延长线交于点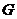 ,若
,若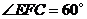 ,连结
,连结 ,判断
,判断 的形状并证明.
的形状并证明.
27.(本小题满分10分)
某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金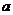 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同,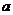 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
28.(本小题满分10分)
直线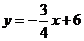 与坐标轴分别交于
与坐标轴分别交于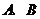 两点,动点
两点,动点 同时从
同时从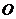 点出发,同时到达
点出发,同时到达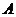 点,运动停止.点
点,运动停止.点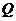 沿线段
沿线段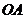 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点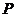 沿路线
沿路线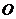 →
→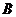 →
→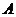 运动.
运动.
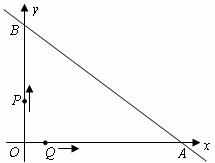
(1)直接写出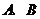 两点的坐标;
两点的坐标;
(2)设点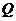 的运动时间为
的运动时间为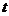 秒,
秒,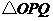 的面积为
的面积为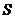 ,求出
,求出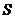 与
与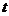 之间的函数关系式;
之间的函数关系式;
(3)当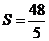 时,求出点
时,求出点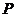 的坐标,并直接写出以点
的坐标,并直接写出以点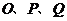 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标.
的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com