
2009年湖北省宜昌市初中毕业生学业考试数学试卷
本试卷共24小题,满分120分,考试时间120分钟.
注意事项:
本试卷分试题卷和答题卡两部分,请将答案答在答题卡上每题对应的答题区域内,答在试题卷上无效.
考试结束,请将本试题卷和答题卡一并上交.
以下数据、公式供参考:
二次函数y=ax2+bx+c图象的顶点坐标是( );
);
 (R为半径,l为弧长); sin30°=
(R为半径,l为弧长); sin30°= , cos30°=
, cos30°= , sin45°=cos45°=
, sin45°=cos45°= .
.
一、选择题(在各小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡上指定的位置填涂符合要求的选项前面的字母代号. 本大题共10小题,每题3分,计30分)
1.如下书写的四个汉字,其中为轴对称图形的是( )

A. B. C. D.
2.如果+20%表示增加20%,那么-6%表示( )
A.增加14% B.增加6% C.减少6% D.减少26%
3.如图所示的圆柱体,其主视图、左视图和俯视图中至少有一个是( )

A.三角形 B.四边形 C.五边形 D.六边形
4.2009年国家将为医疗卫生、教育文化等社会事业发展投资1 500亿元。将1 500用科学记数法表示为( )
A.1.5×10-3 B.0.15×
5.某市决定从桂花、菊花、杜鹃花中随机选取一种作为市花,选到杜鹃花的概率是( ).
A.1 B.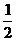 C.
C.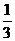 D.0
D.0
6.按如图方式把圆锥的侧面展开,会得到的图形是( ).


A. B. C. D.
7.如果ab<0,那么下列判断正确的是( ).
A.a<0,b<0 B.a>0,b>
8.如图,由“基本图案”正方形ABCO绕O点顺时针旋转90°后的图形是 ( ).
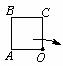 基本图案
基本图案
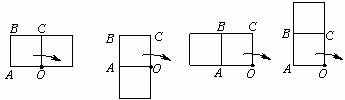
A. B. C. D.
9.设方程x2-4x-1=0的两个根为x1与x2,则x1x2的值是( )
A.-4 B.-
10.由于干旱,某水库的蓄水量随时间的增加而直线下降,若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
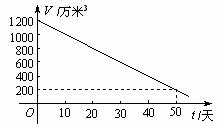
A.干旱开始后,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1 200万米3
二、填空题(请将解答结果填写在答题卡上指定的位置.本大题共5小题,每题3分计15分)
11.当x= 时,分式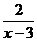 没有意义.
没有意义.
12.“爱心小组”的九位同学为灾区捐款,捐款金额分别为10,10,11,15,17,17,18,20,20 (单位:元).那么这组数据的中位数是 .
13.如果只用圆、正五边形、矩形中的一种图形镶嵌整个平面,那么这个图形只能是 .
14.如图,日食图中表示太阳和月亮的分别为两个圆,这两个圆的位置关系是 .

15.如图,艳军中学学术报告厅门的上沿是圆弧形,这条弧所在圆的半径为

三、解答题(本大题共9小题,计75分)
16.化简: 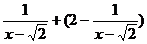 . (6分)
. (6分)
17.2009年有80名教师参加“城乡教师援助工程”活动,随机调查后发现,平均每位教师可以让150名学生受益.请你估算有多少学生将从这项活动中受益. (6分)
18.已知点A(1,-k+2)在双曲线 上,求常数k的值. (7分)
上,求常数k的值. (7分)
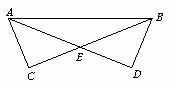
19.已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长. (7分)
20.已知:如图,⊙O的直径AD=2,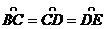 ,∠BAE=90°.
,∠BAE=90°.
(1)求△CAD的面积;
(2)如果在这个圆形区域中,随机确定一个点P,那么点P落在四边形ABCD区域的概率是多少? (8分)
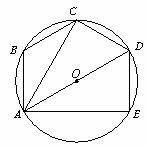
21.已知:如图,AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF, AF相交于P,M.
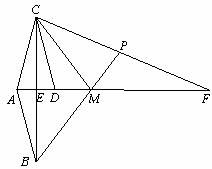
(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.(8分)
22.【实际背景】
预警方案确定:
设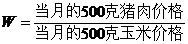 .如果当月W<6,则下个月要采取措施防止“猪贱伤农”.
.如果当月W<6,则下个月要采取措施防止“猪贱伤农”.
【数据收集】
今年2月~5月玉米、猪肉价格统计表
月 份
2
3
4
5
玉米价格(元/
0.7
0.8
0.9
1
猪肉价格(元/
7.5
m
6.25
6
【问题解决】
(1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等,求3月的猪肉价格m;
(2)若今年6月及以后月份,玉米价格增长的规律不变,而每月的猪肉价格按照5月的猪肉价格比上月下降的百分数继续下降,请你预测7月时是否要采取措施防止“猪贱伤农”;
(3)若今年6月及以后月份,每月玉米价格增长率是当月猪肉价格增长率的2倍,而每月的猪肉价格增长率都为a,则到7月时只用5.5元就可以买到
23.已知:如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D,C重合), MN为折痕,点M,N分别在边BC, AD上,连接AP,MP,AM, AP与MN相交于点F.⊙O过点M,C,P。
(1)请你在图1中作出⊙O(不写作法,保留作图痕迹);
(2)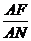 与
与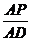 是否相等?请你说明理由;
是否相等?请你说明理由;
(3)随着点P的运动,若⊙O与AM相切于点M时,⊙O又与AD相切于点H.设AB为4,请你通过计算,画出这时的图形.(图2,3供参考) (11分)
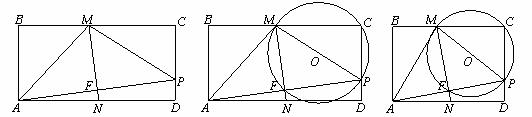
图1 图2 图3
24.已知:直角梯形OABC的四个顶点是O(0,0),A(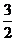 ,1), B(s,t),C(
,1), B(s,t),C(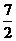 ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
(1)求s与t的值,并在直角坐标系中画出直角梯形OABC;
(2)当抛物线y=x2+mx-m与直角梯形OABC的边AB相交时,求m的取值范围.(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com