
2009年湖北省孝感市初中毕业生学业考试
数学试卷
温馨提示:
1.答题前,考生务必将自己所在县(市、区)、学校、姓名、考号填写在试卷上指定的位置。
2.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题的答案必须写在答题卡的指定位置,在本卷上答题无效。
3.本试卷满分120分,考试时间120分钟。
一、精心选一选,相信自己的判断!(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合题目要求的,不涂、错涂或涂的代号超过一个,一律得0分)
1.-32的值是
A.6 B.-
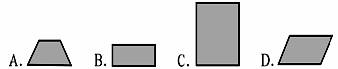
2.小华拿着一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影不可能是
3.如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是
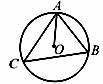
A.15° B.30° C.45° D.60°
4.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒。当你抬头看信号灯时,是绿灯的概率是
A. B.
B.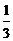 C.
C.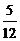 D.
D.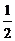
5.如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则B′点的坐标为
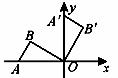
A.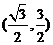 B.
B.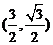 C.
C.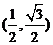 D.
D.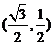
6.某一段时间,小芳测得连续五天的日最低气温后,整理得出下表(有两个数据被遮盖)。
日期
一
二
三
四
五
方差
平均气温
最低气温
1℃
-1℃
2℃
0℃
■
■
1℃
被遮盖的两个数据依次是
A.3℃,2 B.3℃,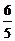 C.2℃,2 D.2℃,
C.2℃,2 D.2℃,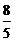
7.如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上。小明认为:若MN = EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN = EF.你认为
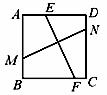
A.仅小明对 B.仅小亮对 C.两人都对 D.两人都不对
8.关于x的方程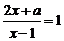 的解是正数,则a的取值范围是
的解是正数,则a的取值范围是
A.a>-1 B.a>-1且a≠0 C.a<-1 D.a<-1且a≠-2
9.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感。如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为

A.4cm B.6cm C.8cm D.10cm
10.将函数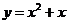 的图象向右平移a
的图象向右平移a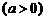 个单位,得到函数
个单位,得到函数 的图象,则a的值为
的图象,则a的值为
A.1 B.2 C.3 D.4
11.如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去了7个小正方体),所得到的几何体的表面积是

A.78 B.72 C.54 D.48
12.对于每个非零自然数n,抛物线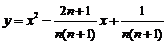 与x轴交于An、Bn两点,以
与x轴交于An、Bn两点,以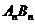 表示这两点间的距离,则
表示这两点间的距离,则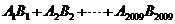 的值是
的值是
A.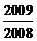 B.
B. C.
C.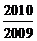 D.
D.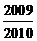
二、细心填一填,试试自己的身手!(本大题共6小题,每小题3分,共18分.请将结果直接填写在答题卡相应位置上)
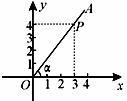
13.如图,角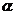 的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则
的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则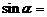 .
.
14.关于x的不等式组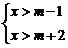 的解集是
的解集是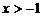 ,则m = .
,则m = .
15.若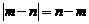 ,且
,且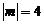 ,
,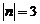 ,则
,则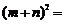 .
.
16.对于任意两个实数对(a,b)和(c,d),规定:
当且仅当a=c且b=d时,(a,b)=(c,d).定义运算“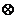 ”:(a,b)
”:(a,b)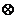 (c,d)=(ac-bd,ad+bc)。若(1,2)
(c,d)=(ac-bd,ad+bc)。若(1,2)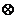 (p,q)=(5,0),则p= ,q= .
(p,q)=(5,0),则p= ,q= .
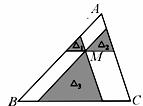
17.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是
.
18.在平面直角坐标系中,有A(3,-2),B(4,2)两点,现另取一点C(1,n),当n = 时,AC + BC的值最小.
三、用心做一做,显显自己的能力!(本大题共7小题,满分66分.解答写在答题卡上)
19.(本题满分6分)
已知: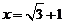 ,
, ,求下列各式的值.
,求下列各式的值.
(1)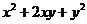 ;(3分)
;(3分)
(2)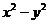 .(3分)
.(3分)
20.(本题满分8分)
三个牧童A、B、C在一块正方形的牧场上看守一群牛,为保证公平合理,他们商量将牧场划分为三块分别看守,划分的原则是:①每个人看守的牧场面积相等;②在每个区域内,各选定一个看守点,并保证在有情况时他们所需走的最大距离(看守点到本区域内最远处的距离)相等.按照这一原则,他们先设计了一种如图1的划分方案:把正方形牧场分成三块相等的矩形,大家分头守在这三个矩形的中心(对角线交点),看守自己的一块牧场.
过了一段时间,牧童B和牧童C又分别提出了新的划分方案.
牧童B的划分方案如图2:三块矩形的面积相等,牧童的位置在三个小矩形的中心.
牧童C的划分方案如图3:把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个人所需走的最大距离相等.
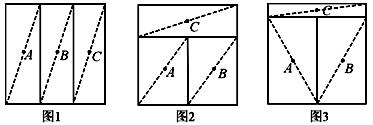
请回答:
(1)牧童B的划分方案中,牧童 (填A、B或C)在有情况时所需走的最大距离较远;(3分)
(2)牧童C的划分方案是否符合他们商量的划分原则?为什么?(提示:在计算时可取正方形边长为2)(5分)
21.(本题满分10分)
某班6名同学组成了一个“帮助他人,快乐自己”的体验小组。他们约定一学期每人至少参加一次公益活动。学期结束后,他们参加公益活动的统计图如下。
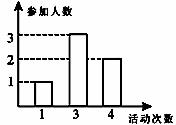
(1)这个体验小组一学期参加公益活动的人均次数是 次;(4分)
(2)从这6名同学中任选两名同学(不考虑先后顺序),他们参加公益活动的次数恰好相等的概率是多少?(6分)
22.(本题满分10分)
如图,⊙O是Rt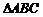 的外接圆,
的外接圆,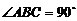 ,点P是圆外一点,PA切⊙O于点A,且PA = PB.
,点P是圆外一点,PA切⊙O于点A,且PA = PB.
(1)求证:PB是⊙O的切线;(5分)
(2)已知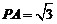 ,
,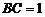 ,求⊙O的半径.(5分)
,求⊙O的半径.(5分)

23.(本题满分10分)
已知抛物线 (k为常数,且k>0).
(k为常数,且k>0).
(1)证明:此抛物线与x轴总有两个交点;(4分)
(2)设抛物线与x轴交于M、N两点,若这两点到原点的距离分别为OM、ON,且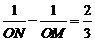 ,求k的值.(6分)
,求k的值.(6分)
24.(本题满分10分)
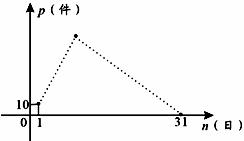
5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
(1)写出p关于n的函数关系式p = (注明n的取值范围);(3分)
(2)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(4分)
(3)该品牌衬衣本月共销售了 件.(3分)
25.(本题满分12分)
如图,点P是双曲线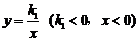 上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=
上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=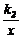 (0<k2<|k1|)于E、F两点.
(0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);(3分)
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;(4分)
②记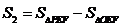 ,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.(5分)
,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com