
2008-2009学年度曲阜市第二学期九年级中考考前检测
数学试卷
考生须知:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共10页.第Ⅰ卷2页为选择题,36分;第Ⅱ卷8页为非选择题,84分;共120分.考试时间为120分钟.
2.第Ⅰ卷每题选出答案后,请把答案标号(ABCD)填写在第Ⅱ卷标定的位置上.
3.答第Ⅱ卷时,将密封线内的项目填写清楚,用钢笔或圆珠笔直接答在试卷上.
第Ⅰ卷(选择题共36分)
一、精心选一选:(本大题共12小题,每题3分,共36分.在每题所给出的四个选项中,只有一项是符合题意的.相信你一定会选对!)
1.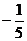 的绝对值是( )
的绝对值是( )
A. B.
B.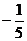 C.5 D.-5
C.5 D.-5
2.北京2008年第29届奥运会火炬接力活动历时130天,传递总里程约13.
A.1.37×10千米 B.1.37×105千米
C.1.37×104千米 D.13.7×104千米
3.某校在“校园十佳歌手”比赛上,六位评委给1号选手的评分如下:90,96,91,96,95,94.那么,这组数据的众数和中位数分别是( )
A.96,94.5 B.96,
4.若关于 的不等式组
的不等式组 有3个整数解,则
有3个整数解,则 的值可以是( )
的值可以是( )
A.-2 B.
5.下列四个图形中,既是轴对称图形,又是中心对称图形的是( )

A.①② B.①③ C.②③ D.①②③
6.在反比例函数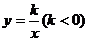 的图象上有两点A(
的图象上有两点A(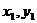 ),B(
),B( ),且
),且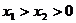 ,
,
则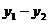 的值为( )
的值为( )
A.正数 B.负数 C.非正数 D.非负数
7.已知抛物线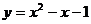 与
与 轴的一个交点为(
轴的一个交点为(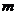 ,0),则代数式
,0),则代数式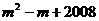 的值为( )
的值为( )
A.2006 B.
8.正方形 中,
中,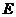 、
、 分别为
分别为 、
、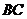 的中点,
的中点,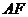 与
与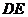 相交于点
相交于点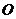 ,则
,则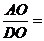 ( )
( )

A. B.
B. C.
C.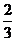 D.
D.
9.已知⊙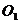 和⊙
和⊙ 的半径分别为
的半径分别为 、
、 ,
,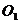
 =
=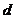 ,且
,且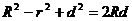 ,则两圆的位置关系是( )
,则两圆的位置关系是( )
A.内含 B.内切 C.相交 D.相切
10.某工件形状如图所示,圆弧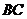 的度数为
的度数为 ,
, 厘米,点
厘米,点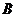 到点
到点 的距离等于
的距离等于 ,则工件的面积等于( )
,则工件的面积等于( )

A.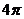 B.
B.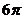 C.
C.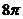 D.
D.
11.下面的三视图所对应的物体是( )
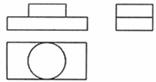

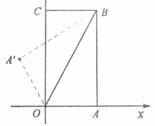
12.如下图,把矩形纸片 放人平面直角坐标系中,使
放人平面直角坐标系中,使 、
、 分别落在
分别落在 轴、
轴、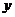 轴上,连接
轴上,连接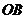 ,将纸片
,将纸片 沿
沿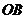 折叠,使点
折叠,使点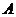 落在点
落在点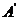 的位置.若
的位置.若 ,tan
,tan 则点
则点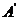 的坐标为( )
的坐标为( )
A.(-1,2) B.( ,
, ) C.(
) C.(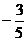 ,
, ) D.(-2,1)
) D.(-2,1)
第Ⅱ卷(选择题共84分)
二、细心填一填:(本大题共有6小题,每题3分,共18分.请把结果直接填在题中的横线上。只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)
13.圆锥的底面半径为
14.掷两枚质地均匀的硬币,则两枚硬币全部正面朝上的概率等于________.
15.如图,一个宽为

16.如图,数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为
17.如图,直线 经过A(-2,-1)和B(-3,0)两点,则不等式组
经过A(-2,-1)和B(-3,0)两点,则不等式组 的解集为________________.
的解集为________________.

18.将正整数按如图所示的规律排列下去。若用有序实数对( )表示第
)表示第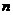 排,从左到右第
排,从左到右第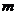 个数,如(4,3)表示实数9,则(7,2)表示的实数是_____________。
个数,如(4,3)表示实数9,则(7,2)表示的实数是_____________。
1 ―――――――――― 第一排
2 3 ――――――――― 第二排
4 5 6 ―――――――― 第三排
7 8 9 10 ――――――― 第四排
……
三、认真答一答:(本大题8小题,满分66分.只要你认真思考,仔细运算,一定会解答正确的!)
19.(6分)化简求值:用一个你认为合适的 值,求代数式
值,求代数式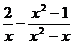 的值。
的值。
20.(8分)某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:
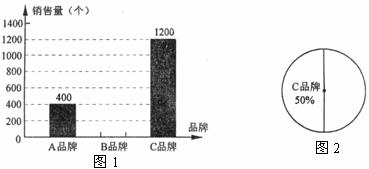
(1)哪一种品牌粽子的销售量最大?
(2)补全图1中的条形统计图.
(3)写出A品牌粽子在图2中所对应的圆心角的度数.
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
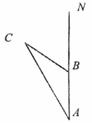
21.(8分)地震发生后,一支专业搜救队驱车前往灾区救援。如下图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西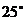 方向,汽车以
方向,汽车以 方向.
方向.
(1)求 处到村庄
处到村庄 的距离;
的距离;
(2)求村庄 到该公路的距离.(结果精确到0.lkm)
到该公路的距离.(结果精确到0.lkm)
(参考数据:sin 4,cos
4,cos 8,sin
8,sin 0,
0,
cos 7)
7)
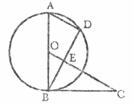
22.(8分)如图所示, 是⊙
是⊙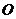 的直径,
的直径,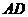 是弦,∠
是弦,∠ =∠
=∠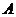 ,
, ⊥
⊥ 于点
于点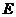 .
.
(1)求证: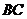 是⊙
是⊙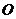 的切线;
的切线;
(2)若 =12,
=12, =10,求
=10,求 的长.
的长.
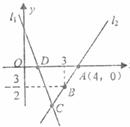
23.(8分)如下图,直线 的解析表达式为
的解析表达式为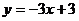 ,且
,且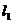 与
与 轴交于点
轴交于点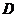 ,直线
,直线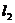 经过点
经过点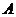 ,
,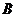 ,直线
,直线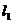 ,
,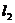 交于点
交于点 .
.
(1)求点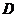 的坐标;
的坐标;
(2)求直线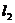 的解析表达式;
的解析表达式;
(3)求△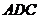 的面积;
的面积;
(4)在直线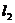 上存在异于点
上存在异于点 的另一点
的另一点 ,使得△
,使得△ 与△
与△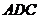 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.
24.(8分)某航运公司年初用120万元购进―艘运输船,在投入运输后,每一年的总收人为72万元,需要支出的各种费用为40万元。
(1)问:该船运输几年后开始盈利(盈利即指总收入减去购船费及所有支出费用之差为正值)?
(2)若该船运输满15年要报废,报废时旧船卖出可收回20万元,求这15年平均盈利额(精确0.1万元)。
25.(10分)用两个全等的等边△ 和△
和△ 拼成如图的菱形
拼成如图的菱形 。现把一个含
。现把一个含 角的三角板与这个菱形叠合,使三角板的
角的三角板与这个菱形叠合,使三角板的 角的顶点与点
角的顶点与点 重合,两边分别与
重合,两边分别与 、
、 重合。将三角板绕点
重合。将三角板绕点 逆时针方向旋转。
逆时针方向旋转。
(1)当三角板的两边分别与菱形的两边 、
、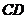 相交于点
相交于点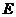 、
、 时(图a)
时(图a)
①猜想 与
与 的数量关系是_________________;
的数量关系是_________________;
②证明你猜想的结论。

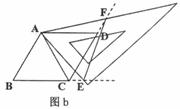
(2)当三角板的两边分别与菱形的两边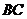 、
、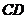 的延长线相交于点
的延长线相交于点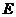 、
、 时(图b),连结
时(图b),连结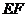 ,判断△
,判断△ 的形状,并证明你的结论。
的形状,并证明你的结论。
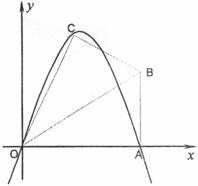
26.(10分)已知,在Rt△OAB中,∠OAB= ,∠BOA=
,∠BOA= ,AB=2。若以O为坐标原点,OA所在直线为
,AB=2。若以O为坐标原点,OA所在直线为 轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
(1)求点C的坐标;
(2)若抛物线 经过C、A两点,求此抛物线的解析式;
经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作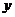 轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
注:抛物线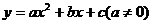 的顶点坐标为(
的顶点坐标为(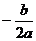 ,
, ),对称轴公式为
),对称轴公式为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com