
2009年深圳市初中毕业生学业考试
数学试卷
一、选择题(本题共10小题,每小题3分,共30分,每小题给出四个选项,其中只有一个是正确的)
1.3的倒数是
A.一3 B.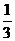 C.一
C.一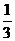 D.3
D.3
2.经公安部交管局统计,今年5月份全国因道路交通事故造成伤亡25 591人,这个数据用科学记数法可以表示为
A.2.559 1×105 B.25.591×103 C.2.559 1×104 D.2.559 1×106
3.如图,平放在台面上的圆锥体的主视图是
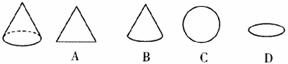
4.下列图形中,既是轴对称图形,又是中心对称图形的是
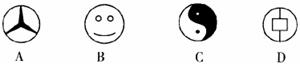
5.某烟花爆竹厂从20万件同类产品中随机抽取了l00件进行质检,发现其中有5件不合格,那么你估计该厂这20万件产品中合格品约为
A.1万件 B.19万件 C.15万件 D.20万件
6.化简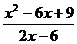 的结果是
的结果是
A.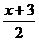 B.
B.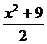 C.
C.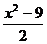 D.
D.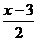
7.班长去文具店买毕业留言卡50张,每张标价2元,店老板说可以按标价九折优惠,则班长应付
A.45元 B.90元 C.10元 D.100元
8.二次函数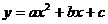 的图象如图所示,若点A(1,y1)、B(2,y2)是它图象上的两点,则y1与y2的大小关系是
的图象如图所示,若点A(1,y1)、B(2,y2)是它图象上的两点,则y1与y2的大小关系是
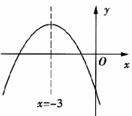
A.y1<y2 B.y1=y
9.不等式组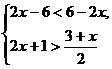 的整数解
的整数解
A.1,2
B.1,2,3 C.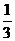 <
<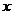 <3 D.0,l,2
<3 D.0,l,2
10.如图,在矩形ABCD中,DE⊥AC于E.∠EDC:∠EDA=1:3。且AC=10,则DE的长度是
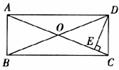
A.3 B.5
C.5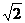 D.
D.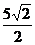
二、填空题(本题共6小题,每小题3分,共18分)
11.计算: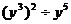 =_______________.
=_______________.
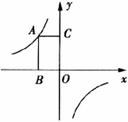
12.如图,A为反比例函数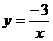 的图象在第二象限上的任一点,AB⊥
的图象在第二象限上的任一点,AB⊥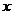 轴于B,AC⊥y轴于C.则矩形ABOC的面积S=_________.
轴于B,AC⊥y轴于C.则矩形ABOC的面积S=_________.
13.为了准备毕业联欢的抽奖活动,小华准备了l0个白球,2个红球,8个黄球,每个球除颜色外其他都相同,把它们放入不透明的口袋中搅匀,规定每位同学每次抽奖,只能从袋中摸出一个球,记下颜色后放回,摸到红球可获钢笔一支.那么小亮抽奖一次得到钢笔的概率是__________.
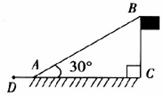
14.如图,小明利用升旗用的绳子测量学校旗杆BC的高度,他发现绳子刚好比旗杆长11米,若把绳子往外拉直,绳子接触地面A点并与地面形成30°角时,绳子末端D距A点还有1米,那么旗杆BC的高度为_______________.
15.下面是按一定规律摆放的图案,按此规律,第2 009个图案与第1~4个图案中相同的是___________.(只填数字)

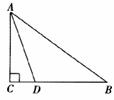
16.如图,在Rt△ABC中,∠C=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=__________.
三、解答题(本题共7小题,其中第17题5分,第18题6分,第19题6分,第20题8分,第21题8分,第22题9分,第23题10分,共52分)
17.(本题5分)计算: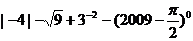 .
.
18.(本题6分)解分式方程: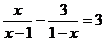 .
.
19.(本题6分)随着网络的普及,越来越多的人喜欢到网上购物.某公司对某个网站2005年到2008年网上商店的数量和购物顾客人次进行了调查.根据调查结果,将四年来该网站网上商店的数量和每个网上商店年平均购物顾客人次分别制成了折线统计图和条形统计图.请你根据统计图提供的信息完成下列填空:
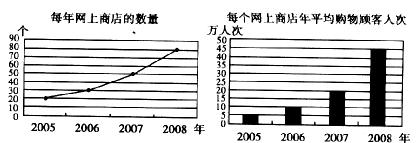
(1)2005年该网站共有网上商店_________个;
(2)2008年该网站网上购物顾客共有_________万人次;
(3)这四年该网站平均每年网上购物顾客有_________万人次.
10.(本题8分)如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
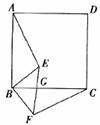
(1)求证:△ABE≌△CBF;
(2)若∠ABE=50°,求∠EGC的大小.
21.(本题8分)如图,AB是⊙O的直径,AB=10,DC切⊙O于点C,AD⊥DC,垂足为D,AD交⊙O于点E.
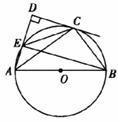
(1)求证:AC平分∠BAD;
(2)若sin∠BEC=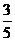 ,求DC的长.
,求DC的长.
22.(本题9分)某汽车制造厂开发了一款新电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:l名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2 000元的工资,给每名新工人每月发1 200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
23.(本题l0分)已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与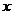 轴重合(其中OA<OB),直角顶点在y轴正半轴上(如图(1)).
轴重合(其中OA<OB),直角顶点在y轴正半轴上(如图(1)).
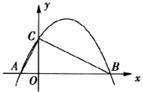
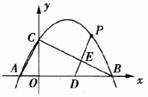
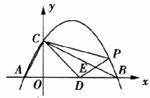
图(1) 图(2) 图(3)
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图(2),点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标
②又连接CD、CP(如图(3)),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com