
2009年江苏名校高中单独招生考试(二)
数学试卷
(本试卷满分100分,考试时间90分钟)
第Ⅰ卷(选择题共18分)
一、选择题(本大题共6小题,每小题3分,共18分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在如图所示的方格纸中,每个小正方形的边长为1,如果以MN所在的直线为y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则这时C点的坐标可能是 ( )
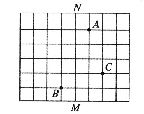
A.(1,3) B.(2,-1) C.(2,1) D.(3,1)
2.某轮船往返于A,B两地之间,设轮船在静水中的速度不变,那么,当水的流速增大时,轮船往返一次所用的时间 ( )
A.不变 B.增加 C.减少 D.增加、减少都有可能
3.已知关于x的方程(m一2)2x2+(
A.m<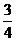 B.m≤
B.m≤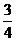 C.m>
C.m>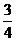 且m≠2 D.m≥
且m≠2 D.m≥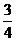 且m≠2
且m≠2
4.已知关于x的方程mx+2=2(m-x)的解满足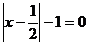 ,则m的值是 ( )
,则m的值是 ( )
A.10或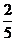 B.10或
B.10或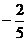 C.-10或
C.-10或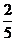 D.-10或
D.-10或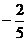
5.如果多项式P=a2+2b2+
A.2005 B.
6.已知a-b=4,ab+c2+4=0,则a+b的值为 ( )
A.4 B.
第Ⅱ卷(非选择题 共82分)
二、填空题(本大题共12小题,每小题4分,共48分.请把答案填在题中横线上)
7.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2008的值为________.
8.若不等式组
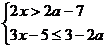 在实数范围内无解,则a的取值范围为________.
在实数范围内无解,则a的取值范围为________.
9.已知:a与b互为相反数,且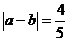 ,则
,则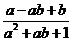 的值为________
的值为________
10.直角坐标系中,以P(2,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为________.
11.在同一坐标系中给出如下四种不同的图象:
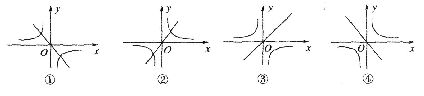
其中有三个可能是正比例函数y=2kx与反比例函数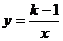 在同一坐标系中的图象,它们的序号是________.
在同一坐标系中的图象,它们的序号是________.
12.一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是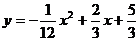 .则他将铅球推出的距离是________m.
.则他将铅球推出的距离是________m.
13.已知点P是半径为5的⊙O内一定点,且PO=4,则过点P的所有弦中,弦长可取到的整数值共有的条数是________.
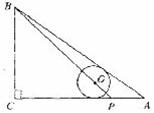
14.如下图,在△ABC中,∠C=900,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是________,
15.设多项式ax5+bx3+cx+d=M,已知当x=0时,M=-5;当x=-3时,M=7,则当x=3时,M=________.
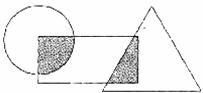
16.如图圆中的阴影部分面积占圆面积的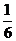 ,占长方形面积的
,占长方形面积的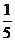 ;三角形中阴影部分面积占三角形面积的
;三角形中阴影部分面积占三角形面积的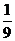 ,占长方形面积的
,占长方形面积的 .则圆、长方形、三角形的面积比________
.则圆、长方形、三角形的面积比________
17.已知x+2y一6z=0,3x-y=4z,则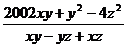 的值为________.
的值为________.
18.如果对于任意两个实数a,b,“*”为一种运算,定义为a*b=a+2b,则函数,y=x2
*(2x)+2*4(一3≤x≤3)的最大值与最小值的和为________.
三、解答题(本大题共4小题,共34分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分8分)
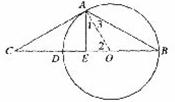
如图,过⊙O上一点A的切线AC与⊙O直径BD的延长线交于点C,过A作AE⊥BC于点E.
(1)求证:∠CAE =2∠B;
(2)已知:AC=8,且CD=4,求⊙O的半径及线段AE的长.
20.(本小题满分8分)
在某文具商场中,每个画夹定价为20元,每盒水彩定价为5元.为促进销售,商场制定两种优惠方案:一种是买一个画夹赠送一盒水彩;另一种是按总价92%付款.一个美术教师欲购买画夹4个,水彩若干盒(不少于4盒).
(1)设购买水彩数量为x(盒),付款总金额为y(元),分别建立两种优惠方案中的y与x的函数关系式;
(2)如果购买同样多的水彩,哪种方案更省钱?
21.(本小题满分8分)
实数x与y使得x+y,x-y,xy,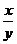 四个数中的三个有相同的数值,求出所有具有这样性质的数对(x,y).
四个数中的三个有相同的数值,求出所有具有这样性质的数对(x,y).
22.(本小题满分10分)
如图,在⊙M中,弧AB所对的圆心角为1200,已知圆的半径为
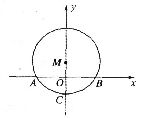
(1)求圆心M的坐标;
(2)求经过A,B,C三点的抛物线的解析式;
(3)点D是弦AB所对的优弧上一动点,求四边形ACBD的最大面积;
(4)在(2)中的抛物线上是否存在一点P,使△PAB和△ABC相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com