
2008-2009学年度江苏省盐城市初级中学第二学期初二期末考试
数学试卷
(考试时间:120分钟 卷面总分:150分)
一、精心选一选(本大题共有10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填在题后的括号内。只要你掌握概念,认真思考,相信你一定会选对的!)
1.下列事件为必然事件的是( )
A.买一张电影票,座位号是偶数 B.抛掷一枚普通的正方体骰子1点朝上
C.百米短跑比赛,一定产生第一名 D.明天会下雨
2.如图,CD∥EF,AB分别交CD、EF于M,N两点,∠AMD=60°,则∠ANF=( )
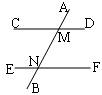
A.60° B.120° C.50° D.130°
3.在比例尺为1:5000的地图上,量得甲,乙两地的距离
A.
4.下列计算中,正确的是 ( )
A.2+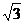 =
=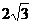 B.
B.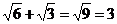
C.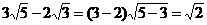 D.
D.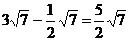
5.如图,下列条件中不能确定四边形ABCD是平行四边形的是 ( )
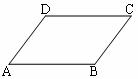
A.AB=CD,AD∥BC B.AB=CD,AB∥CD
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
6.估计无理数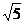 的值应在 ( )
的值应在 ( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
7.如图,一油桶高0.
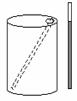
A.0.
8.如图,一个角为60°的直角三角形纸片,沿其一条中位线剪开,不能拼成的四边形是( )
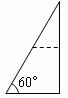
A.邻边不等的矩形 B.等腰梯形
C.有一个角是锐角的菱形 D.正方形
9.如图,矩形ABCD沿AE折叠,使D落在边BC上的F点处,如果∠BAF=60°,则∠DAE=
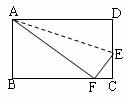
A.15° B.20° C.25° D.30°
10.如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB,AC分别平行于x轴,y轴,若双曲线y=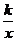 (k≠0)与△ABC有交点,则k的取值范围是
( )
(k≠0)与△ABC有交点,则k的取值范围是
( )
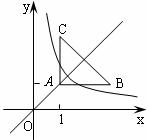
A.1<k<2 B.1≤k≤
二、细心填一填(本大题共有8小题,8个空,每空3分,共24分.请把结果直接填在题中的横线上。只要你理解概念,仔细运算,相信你一定会填对的!)
11.函数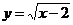 中,自变量x的取值范围是_____________.
中,自变量x的取值范围是_____________.
12.某等腰三角形的两条边长分别为
13.一布袋中有红球8个,白球5个和黑球12个,它们除颜色外没有其他区别,随机地从袋中取出1球不是黑球的概率为______________.
14.在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积v时,气体的密度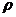 也随之改变.
也随之改变.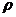 与v在一定范围内满足
与v在一定范围内满足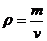 ,图象如图所示,该气体的质量m为
____________kg.
,图象如图所示,该气体的质量m为
____________kg.
15.若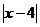 +
+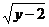 =0,则
=0,则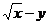 .
.
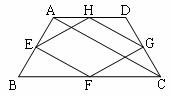
16.某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为
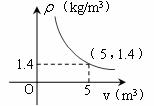
17.已知实数a、b在数轴上对应点的位置如下图,化简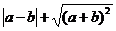 的结果为
.
的结果为
.
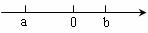
18.如图,正方形A1B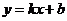 (k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是
.
(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是
.
三、认真答一答(本大题有10小题,共96分.解答时需写出必要的文字说明.演算步骤或证明过程.只要你积极思考,细心运算,你一定会解答正确的!)
19.(本大题共18分,每小题6分)
1.计算:(1)(6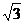 ―3
―3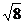 )―(
)―(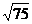 ―
―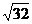 );
);
(2)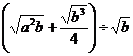
2.先化简,再求值: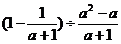 ,其中
,其中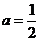 .
.
20.(本题6分)如图,AC=DF,∠A=∠D,AE=DB,那么BC与EF的大小关系如何?说明理由.
21.(本题6分)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?
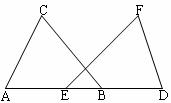
22.(本题8分)小玲用下面的方法来测量学校教学楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学楼的距离EA=
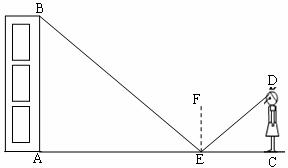
23.(本题8分)已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
(1)说明:AM=DM;
(2)若DF=2,求菱形ABCD的周长.
24.(本题8分)有一枚均匀的正四面体,四个面上分别标有数字l,2,3,4,小红随机地抛掷一次,把着地一面的数字记为x;另有三张背面完全相同,正面上分别写有数字-2,-l,1的卡片,小亮将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后他们计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)分别求出当S=0和S<2时的概率.
25.(本题8分)如图,等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB?CE.
(1)说明:△ADB∽△EAC;
(2)若∠BAC=40°,求∠DAE的度数.
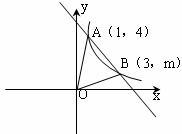
26.(本题10分)如图所示,在直角坐标系xOy中,一次函数y1=k1x+b (k≠0)的图象与反比例函数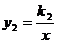 (x>0)的图象交于A(1,4),B(3,m)两点.
(x>0)的图象交于A(1,4),B(3,m)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)在第一象限内, x取何值时,一次函数的函数值大于反比例函数的函数值;
(3)求△AOB的面积.
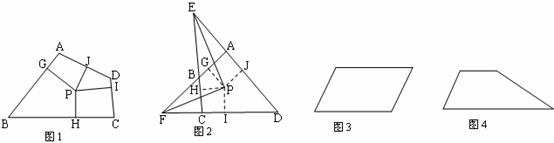
27.(本题12分)定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,,则点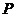 就是四边形ABCD的准内点.
就是四边形ABCD的准内点.
(1)如图2,∠AFD与∠DEC的角平分线FP,EP相交于点P.
求证:点P是四边形ABCD的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”。
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若P是任意凸四边形ABCD的准内点,则PA+PB=PC+PD或PA+PC=PB+PD.( )
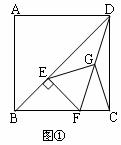
28.(本题12分)如图,已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
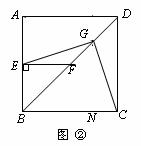
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
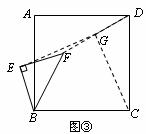
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com