
2008-2009学年度夏津第二学期八年级期终质量检测
数学试卷
时间:120分钟 满分:120分
第Ⅰ卷(选择题 共24分)
一、选择题.(本大题共8小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分)
1.在式子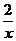 ,
, ,
, ,
,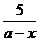 ,
, 中是分式的共有
中是分式的共有
A.2个 B.3个 C.4个 D.5个
2.小马虎在下面的计算中作对了一道题,他作对的题目是
A.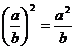 B.
B.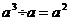 C.
C.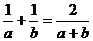 D.
D.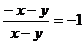
3.下列命题中,正确的命题是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直且相等的四边形是正方形
C.两条对角线互相垂直的四边形是菱形
D.两条对角线互相平分的四边形是平行四边形
4.在等腰梯形ABCD中,AD//BC,AD<BC,AB=2,BC=4,∠B=60°,则该梯形的面积是( )
A.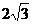 B.
B.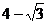 C.
C.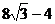 D.3
D.3
5.反比例函数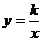 与正比例函数
与正比例函数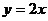 图像的一个交点的横坐标为1,则反比例函数的图像大致为( )
图像的一个交点的横坐标为1,则反比例函数的图像大致为( )
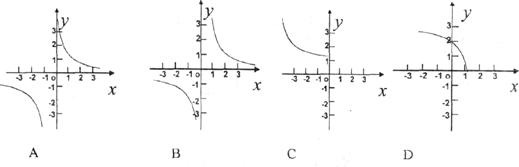
6.若点(-2,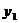 ),(-1,
),(-1,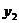 ),(1,
),(1, )在反比例函数
)在反比例函数 图像上,则下列结论中正确的是( )
图像上,则下列结论中正确的是( )
A. B.
B.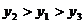 C.
C.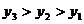 D.
D.
7.甲乙两人各射靶5次,已知甲所中环数是8,7,9,7,9,乙所中环数的甲均数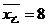 ,方差
,方差 ,那么对甲、乙的射击成绩的正确判断是( )
,那么对甲、乙的射击成绩的正确判断是( )
A.甲的射击成绩较为稳定 B.乙的射击成绩较为稳定
C.甲、乙的射击成绩同样稳定 D.甲、乙的射击成绩无法比较
8.在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边AB翻折后得到△ABC’,则CC’的长等于( )
A. B.
B.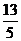 C.
C.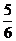 D.
D.
第Ⅱ卷(非选择题 共96分)
二、填空题:(本大题8个小题,每小题4分,共32分)请将答案直接填写在题后的横线上,只要求填写最后结果.
9.当_________时,分式 有意义;当_________时,分式
有意义;当_________时,分式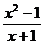 的值为零.
的值为零.
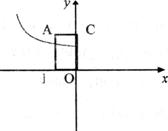
10.如图所示,设A为反比例函数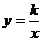 图像上一点,且矩形ABOC的面积为6,则这个反比例函数解析式为______________.
图像上一点,且矩形ABOC的面积为6,则这个反比例函数解析式为______________.
11.自从扫描隧道显微镜发明盾,世界上便诞生了一门新科学,这就是“纳米技术”,已知52个纳米的长度为0.
12.如下图,已知OA=OB,那么数轴上点A所表示的数是__________.

13.在□ABCD中,∠A,∠B的度数比为5:4,则∠C等于___________.
14.有两块面积相同的小麦试验田,第一块与第二块分别收获小麦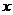 kg,根据题意,可得方程_________________.
kg,根据题意,可得方程_________________.
15.如果△ABC的三边长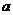 ,b,c满足关系式
,b,c满足关系式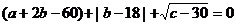 ,则
,则 ________,
________, __________,
__________, ________,△ABC是___________三角形.
________,△ABC是___________三角形.
16.已知,如图,正方形ABCD中,O是对角线AC,BD的交点,过O作OE⊥OF分别交AB、BC于E、F,若AE=12,CF=5,则EF=___________.

三、解答题(本题共7小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤.)
17.(本题满分6分)
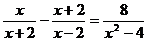
18.(本题满分8分).
先化简再求值,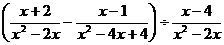 ,其中
,其中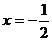 。
。
19.(本题满分8分,请写明必要的解答过程)
下面是某家餐馆所有工作人员某个月的工资(单位:元)
员工
经理
厨师A
厨师B
职员A
职员B
月工资数
2000
850
800
320
320
员工
职员C
职员D
职员E
职员F
职员G
月工资数
350
320
410
500
330
(1)餐馆所有员工的平均工资是_________元.
(2)所有员工工资的中位数是________,众数是_________.
(3)用平均数、中位数还是众数描述餐馆员工工资水平比较恰当?
(4)去掉经理的工资后其他员工的平均工资是___________元,是否也能反映该餐馆员工工资的一般水平?(工资取整数)
20.(本题满分10分)
已知如图,各图形被一条直线将其面积平分。


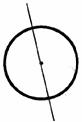
(1)求证:在平行四边形中,过对角线交点的一直线,平分此平行四边形的面积.
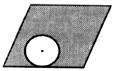
(2)观察上面图形,用所得的结论或启示,对下图所示的每一个图形做一条直线,将其阴影部分面积平分,(不写画法,不用证明,保留作图痕迹)


21.(本题满分9分)
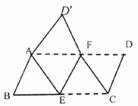
将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D’处,折痕为EF,连接CF,判断四边形AECF是什么特殊的四边形?证明你的结论.
22.(本题满分11分)
已知:正方形ABCD中,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,当∠MAN绕点A旋转到BM=DN时,如图1,
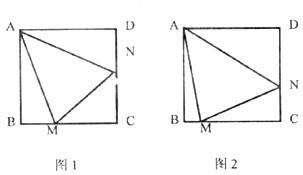

(1)求证BM+DN=MN
(2)当∠MAN绕点A旋转到BM≠DN时,如图2,线段BM、DN和MN之间有怎样的数最关系?写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到图3的位置时,线段BM,DN和MN之间有怎样的数量关系?请直接写出你的猜想.
23.(本题满分l2分)
如图,已知一次函数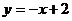 的图像与反比例函数的图像交于A,B两点,且A点的横坐标与B点的纵坐标都是-2.
的图像与反比例函数的图像交于A,B两点,且A点的横坐标与B点的纵坐标都是-2.
求:(1)A点和B点的坐标.
(2)反比例函数的解析式.
(3)△AOB的面积.
(4)探索在坐标轴上是否存在一点P使得△APB的面积为9,若存在,请直接写出坐标;若不存在请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com