
2008-2009学年度德州市夏津第二学期七年级期终质量检测
数学试卷
时间:120分钟 满分:120分
第Ⅰ卷(选择题 共24分)
一、选择题.(本大题共8小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分)
1.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )

A.0 B.
2.如图,一扇窗户打开后,有窗钩AB可将其固定,这里所运用的数学道理是( )

A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图是小刚画的一张脸,他对妹妹说:如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )

A.(2,1) B.(2,2) C.(1,2) D.(2,3)
4.在平面直角坐标系中,若点P( ,
,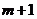 )在第二象限,则
)在第二象限,则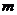 的取值范围为( )
的取值范围为( )
A. B.
B.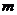 >
>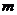 <-l D.
<-l D.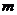 >-l
>-l
5.有两根木棒,它们的长分别是
A.
6.如果∠l与∠2互补,∠l与∠3互余,那么 ( )
A.∠2>∠3 B.∠2=∠
7.已知三角形的三个顶点坐标分别是(-4,-l),(1,1),(-1,4)现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A.(-2,2),(3,4),(1,7); B.(-2,2),(4,3),(1,7);
C.(2,2),(3,4),(1,7): D.(2,-2),(3,3),(1,7)
8.如图,在锐角△ABC中,CD、BE分别是AB、AC边上的高,且相交于一点P,若∠A=50°,则∠BPC的度数是( )
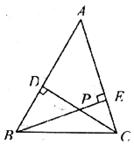
A.150° B.130° C.120° D.100°
第Ⅱ卷(非选择题 共96分)
二、填空题:(本大题8个小题,每小题4分,共32分)请将答案直接填写在题后的横线上,只要求填写最后结果.
9.已知点A(-1, +2)在坐标轴上,则
+2)在坐标轴上,则 =____________.
=____________.
10.如图,字母“M”左右两边的竖线互相平行,∠1+∠2=60°,那么∠3=__________.

11.如果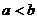 ,那么
,那么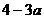 ________
________ .
.
12.石板加工厂有等边三角形、正五边形、正六边形、正方形四种正多边形石板料,现想选用某一种来铺地板(不留空隙),则这四种石板中不能选用的是__________.
13.如图,已知AB//CD,BE平分∠ABC,∠CDE=150°,则∠C=________.

14.若 ,则
,则 ________,
________,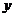 =________.
=________.
15.设●、■、▲分别表示三种不同的物体,如图,前两架天平保持平衡,如果要使第(3)架也平衡,那么“?”处应放“■”的个数为__________.

16.在一个样本中,50个数据分别落在5个小组内,第1,2,3,5,小组数据的个数分别是2,8,15,5,则第4小组的频数是____________。
三、解答题(本大题共7个小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤。)
17.(本题满分l2分)
(1)解不等式 (5分)
(5分)
(2)解不等式组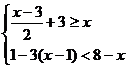 ①②并把它的解集在数轴上表示出来。(7分)
①②并把它的解集在数轴上表示出来。(7分)

18.(本题满分6分)如图,将三角形ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的三角形AlBlC1,画出三角形AlBlC1,并写出点Al、Bl、Cl的坐标。
19.(本题满分8分)
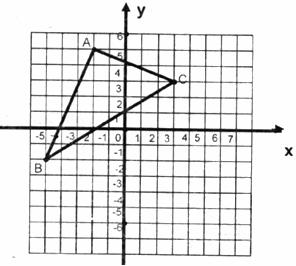
如图,CD//AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
20.(本题满分10分)
甲,乙联赛中,某足球队按足协的计分规则与本队奖励方案如下表.
胜一场
平一场
负一场
积分
3
1
0
奖金(元/人)
1500
700
0
当比赛进行到第12轮结束时,该队负3场,共积19分.
问:(1)该足球队胜了几场,平了几场?(8分)
(2)若每赛一场,每名参赛队员均得出场费500元,试求该队每名队员在l2轮比赛结束后总收入.(2分)
21.(本题满分8分)
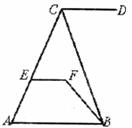
如图,△ABC中,BD是∠ABC的角平分线,DE//BC,交AB于E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.

22.(本题满分8分)
为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图。如下所示:
组别
次数
频数(人数)
第1组
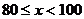
6
第2组
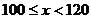
8
第3组


第4组

18
第5组

6

请结合图表完成下列问题:
(1)表中的 =__________;
=__________;
(2)请把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳次数( )达标要求是:
)达标要求是: <120不合格;
<120不合格; 为合格;
为合格; 为良;
为良;
 160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议:__________________________
160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议:__________________________
23.(本题满分l2分)
已知如图l,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并 且与CD、AB分别相交于M、N.试解答下列问题:

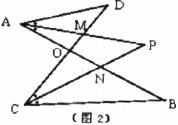
(1)在图1中,∠A、∠B、∠C、∠D之间存在着怎样的数量关系?
(2)仔细观察,在图2中“8字形”的个数:_________个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com