
2008-2009学年度菏泽市郓城第二学期九年级期中质量检测
数学试卷
(满分:120分 时间:120分钟)
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确的选项的代号填入该小题后的括号内,每小题得3分,否则不得分,本大题共30分)
1.下列计算正确的是 ( )
A.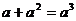 B.
B. C.
C.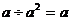 D.
D.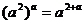
2.某市的耕地面积为7136000公亩,这个数字用科学计数法可表示为 ( )
A.7.136×106 B.7136×
3.以下所述的几何图形既是轴对称图形,又是中心对称图形的是 ( )
A.平行四边形 B.等腰梯形 C.等边三角形 D.正方形
4.如图,AB、CD交于O,OB平分∠DOE,如果∠AOC=35°,则∠COE的度数为 ( )
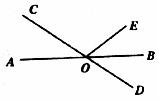
A.95° B.105° C.110° D.120°
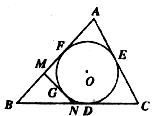
5.如图,圆O是△ABC的内切圆。D、E、F为切点,AB=
A.
6.在同一直角坐标系中,函数 与
与 的图象大致是下面的 ( )
的图象大致是下面的 ( )

7.某人骑车行驶路程S(千米)与时间t(小时)之间的关系如函数图象所示,则以下说法错误的是( )
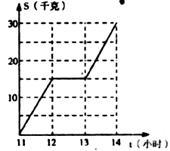
A.从11时到l4时共行驶了30千米
B.从l2时到l3时匀速前进
C.整个行驶过程中的平均速度是10千米/小时
D.从l3时到14时的行驶速度与11时到l2时的行驶速度相同
8.某商场的促销办法是:每10000张奖券为一个开奖组,设一等奖5名,二等奖50名,三等奖100名,凡购物满l00元者均送奖券一张,那么买100元商品的中奖概率为( )
A. B.
B. C.
C.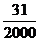 D.
D.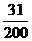
9.如下图,△ABC中,∠C=90°,AC=
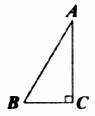
A. cm2 B.
cm2 B. cm2 C.
cm2 C. cm2 D.2
cm2 D.2 cm2
cm2
10.如下图,四边形ABCD中,Q为BC的中点,E、F分别是AP、QP的中点,P为CD边上的一个动点,当点P在CD上由C向D的移动中,则有 ( )
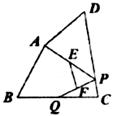
A.线段EF的长度由小变大 B.线段EF的长度由大变小
C.线段EF的长度保持不变 D.线段EF的长度有时变大,有时变小
11.如下图,AB是圆O的弦,D是AB的中点,连结DO并延长交圆O于点C,若AB=12cm,CD=10cm,则圆O的半径OA的长为 ( )
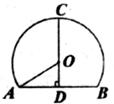
A.8cm B.6cm C.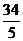 cm D.
cm D. cm
cm
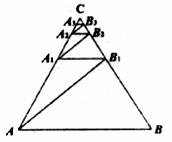
12.如下图,等腰△ABC中,顶角C的正切值tanC= ,过点A作AB1⊥CB于B1,过B1作BlA1//AB,交AC于A1;过点A1作AlB2⊥BC于B2,过B2作A2B2//AB,交AC于A2,如此重复作下去,得△ABB1,△A1BlB2,△A2B2B3……, 设△ABBl,△A1BlB2,△A2B2B3……的面积分别为S1,S2,S3……,则
,过点A作AB1⊥CB于B1,过B1作BlA1//AB,交AC于A1;过点A1作AlB2⊥BC于B2,过B2作A2B2//AB,交AC于A2,如此重复作下去,得△ABB1,△A1BlB2,△A2B2B3……, 设△ABBl,△A1BlB2,△A2B2B3……的面积分别为S1,S2,S3……,则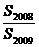 的值为 ( )
的值为 ( )
A.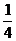 B.
B.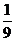 C.
C. D.
D.
二、填空题(每空3分,共24分)
13.将 分解因式得_________________。
分解因式得_________________。
14.函数 中,自变量
中,自变量 的取值范围是___________________。
的取值范围是___________________。
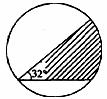
15.一个圆形展览厅如图所示,在其边缘上的点A处安装了一台监视器,它的监控角度是32°,若要监控整个展览厅,至少要在圆形边缘上安装__________台这样的监视器。
16.如图,反比例函数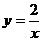 的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4。过这些点分别作
的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4。过这些点分别作 轴与
轴与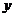 轴的垂线,图中所构成的阴影部分的面积,即从左到右的矩形依次为S1,S2,S3,则S1+S2+S3=____________。
轴的垂线,图中所构成的阴影部分的面积,即从左到右的矩形依次为S1,S2,S3,则S1+S2+S3=____________。

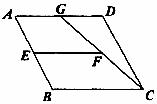
17.如图,平行四边形ABCD中,BC=8cm,G是AD的中点,E、F分别是AB、CG的中点,则EF的长为___________cm
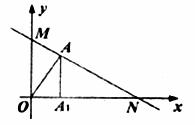
18.如图,函数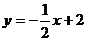 的图象分别交
的图象分别交 轴、
轴、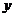 轴于N、M两点,动点A在线段MN上,过A向
轴于N、M两点,动点A在线段MN上,过A向 轴作垂线,垂足为A1,设△OAA1的面积为S,那么,点A在移动的过程中S的最大值为_________________。
轴作垂线,垂足为A1,设△OAA1的面积为S,那么,点A在移动的过程中S的最大值为_________________。
三、解答或证明。
19.本题8分。
先化简,再求值: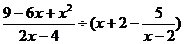 其中
其中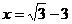 .
.
20.本题10分。
如图,梯形ABCD中,AD//BC,BC=CD,CF平分∠BCD,DF//AB,BF的延长线交DC于E。
求证:(1)∠CBF=∠CDF (2)AD=DE

21.本题10分。
郓城第一初级中学课外体育活动小组,对该校初一年级学生关于象棋、围棋、军棋、跳棋的喜爱情况,在全年级范围内随机抽取了部分同学进行了调查(限每位同学必须只选一种棋类),课外体育活动小组的甲同学根据调查结果计算得知:最喜欢围棋的学生人数占被抽取人数的16%,乙同学根据调查结果绘制成如下不完整的条形统计图:.
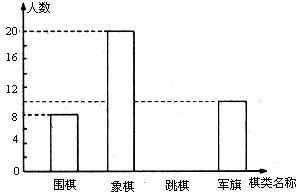
请根据甲、乙两同学提供的信息解答下列问题。
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图的空缺部分;
(3)如果初一年级有1200名学生,请你估计全年级最喜欢跳棋的有多少人?
(4)如果在这个年级中随机的选一名学生,那么可以估计选出的学生是象棋爱好者的概率是多少?
22.本题12分。
某化工厂原来每月利润为120万元,从前年一月起安装了新设备,大大降低了成本,使用新设备后的1至 月(1≤
月(1≤ ≤l2)的利润的月平均值W(万元)满足W=10
≤l2)的利润的月平均值W(万元)满足W=10 +90。
+90。
(1)设使用新设备后的l至 月的利润和为
月的利润和为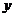 ,写出
,写出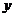 关于
关于 的函数关系武,并求前几个月的利润和为700万元。
的函数关系武,并求前几个月的利润和为700万元。
(2)当 为何值时,使用新设备后的l至
为何值时,使用新设备后的l至 月的利润和与不安装新设备时
月的利润和与不安装新设备时 个月的利润和相等?
个月的利润和相等?
23.本题12分。
如图,圆O的半径为6cm,过圆O外一点P作射线PM、PN,PM经过点O,PN切圆O于Q,A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为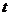 (s).
(s).
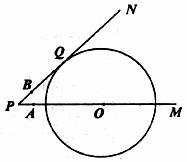
(1)求PQ的长。
(2)当直线AB与圆O相切时,求t的值。
24.本题14分。
如图,二次函数 的图象的顶点坐标为M(2,0),直线
的图象的顶点坐标为M(2,0),直线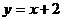 与这个二次函数的图象交于A、B两点,点A在y轴上。
与这个二次函数的图象交于A、B两点,点A在y轴上。

(1)求这个二次函数的解析式。
(2)P为线段AB上异于A、B两点之外的一个动点,过P作 轴的垂线,交抛物线于Q,设线段PQ的长为L,点P的横坐标为
轴的垂线,交抛物线于Q,设线段PQ的长为L,点P的横坐标为 ,求L与
,求L与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围。
的取值范围。
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形,若存在,求出点P的坐标和梯形的面积;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com