
2009年江苏新课标解直角三角形测试(D卷)
数学试卷
一、精心选一选.(每题3分,共30分)
1.已知Rt△ABC中,∠C=90°,tanA=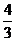 ,BC=8,则AC等于 ( )
,BC=8,则AC等于 ( )
A.6 B.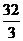 C.10
D.12
C.10
D.12
2.AE、CF是锐角△ABC的两条高,如果AE:CF=3:2,则sinA:sinC等于 ( )
A.3:2 B.2:
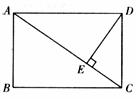
3.如下图,在矩形ABCD中,DE⊥AC于E,设∠ADE=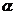 ,且cos
,且cos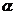 =
=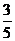 ,AB=4,则AD的长为 ( )
,AB=4,则AD的长为 ( )
A.3 B.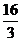 C.
C.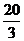 D.
D.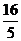
4.已知等腰三角形腰上的高等于腰长的一半,则顶角为 ( )
A.30° B.135° C.150° D.30°或150°
5.如下图,AB//CD,AE⊥CD,AE=12,BD=15,AC=20,则梯形ABCD的面积为 ( )
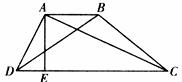
A.130 B.
6.在Rt△ABC中,∠C=90°,cosB=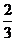 ,则Rt△ABC的三边
,则Rt△ABC的三边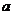 、b、c之比
、b、c之比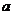 :b:c为 ( )
:b:c为 ( )
A.2: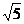 :3 B.1:
:3 B.1: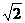 :
: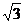
C.1:2:3
D.2: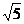 :
: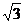
7.若m取大于2的数时,下列四个等式中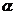 有解的个数是 ( )
有解的个数是 ( )
(1)sin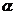 =
=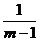 (2)cos
(2)cos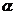 =m一1 (3)tan
=m一1 (3)tan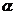 =m+1 (4)tan
=m+1 (4)tan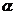 =
=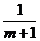
A.1 B.
8.计算:sin20°一cos20°的值是(保留四个有效数字) ( )
A.一0.5976 B.
9.在矩形ABCD中,DE⊥AC于E,设∠ADE=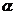 ,且cos
,且cos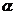 =
=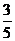 ,AB=4,则AD的长为
( )
,AB=4,则AD的长为
( )
A.3 B.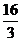 C.
C.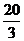 D.
D.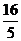
10.如图,在△ABC中,∠C=90°,∠B=50°,AB=10,则BC的长为 ( )
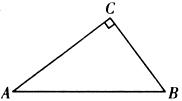
A.10tan50° B.10cos50° C.10sin50° D.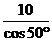
二、耐心填一填.(每题2分,共20分)
11.已知等边三角形的边长为
12.在Rt△ABC中,∠C=90°AB=10,BC=6,则sinA=_________.
13.在Rt△ABC中,∠C=90°,sinA=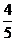 ,tanB=_________.
,tanB=_________.
14.在Rt△ABC中,∠C=90°,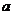 =10,S△ABC=
=10,S△ABC=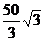 ,则∠A=________.
,则∠A=________.
15.在Rt△ABC中,∠C=90°,∠A=30°,BC=
16.在锐角三角形ABC中,已知| sinA-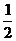 |+(tanB一1)2=0,则∠C=________度.
|+(tanB一1)2=0,则∠C=________度.
17.有一块三角形草坪ABC,∠A=150°,AB=
18.等腰梯形的腰长为6,底角的正切值为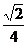 ,下底长为12
,下底长为12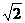 ,则上底长为________,高为________.
,则上底长为________,高为________.
19.如下图,身高
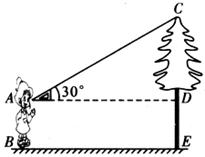
20.课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图,在A处用测角仪(离地高度

三、用心想一想.(共50分)
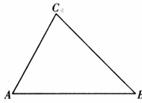
21.(6分)如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求△ABC的面积(结果可保留根号).
22.(6分)如图,在△ABC中,∠C=90°,AC=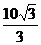 cm,求∠B,AB,BC.
cm,求∠B,AB,BC.
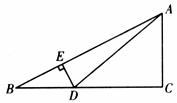
23.(8分)如图,在△ABC中,∠C=90°,D是BC边上一点,DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BE=3,求△ABD的面积.
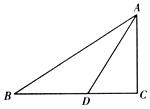
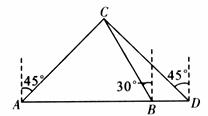
24.(10分)某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°方向,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里,求A、D两点间的距离.
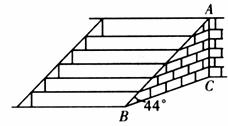
25.(10分)武当山风景管理区为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44°减至32°,已知原台阶AB的长为
(1)改善后的台阶会加长多少?(精确到
(2)改善后的台阶多占多长一段地面?(精确到
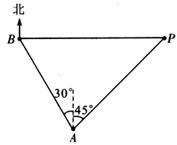
26.(10分)一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,必须进行拦截.巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的P处将走私快艇拦截住.如图所示,试求巡逻艇的速度(结果取整数,参考数据: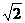 =1.414,
=1.414,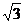 =1.732,
=1.732,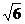 =2.499).
=2.499).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com