
2009-2010学年度福建厦门同安一中第一学期初三期中考试
数学试卷
(本试卷满分150分,考试时间120分钟)
考生注意:本学科考试有两张试卷,分别是本试题(共4页26题)和答题卡。试题答案要填在答题卡相应的答题栏内,否则不能得分。
一、选择题(本大题有7题,每小题3分,共21分。每小题有四个选项,其中有且只有一个选项正确)
1.方程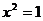 的解是(
)
的解是(
)
A.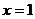 或
或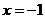 B.
B.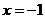
C.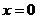 D.
D.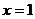
2.下列计算正确的是( )
A.+= B.-=0
C.?=9 D.=-3
3.不解方程,判别方程x2-2x+1=0的根的情况是( )
A.有两个不等实根 B.有两个相等实根
C.没有实根 D.无法确定
4.已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )

A. = B. = C. = D. =
5.某款手机连续两次降价,售价由原来的1185元降到了580元。设平均每次降价的百分率为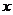 ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A.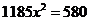 B.
B.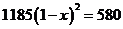
C. D.
D.
6.如图,数轴上点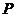 表示的数可能是( )
表示的数可能是( )

A.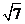 B.
B.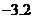 C.
C. D.
D.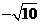
7.若抛物线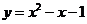 与
与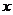 轴的一个交点为
轴的一个交点为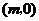 ,则代数式
,则代数式 的值为( )
的值为( )
A.2007 B.
二、填空题(本大题有10小题,每小题4分,共40分)
8.计算:(1) (2)
(2)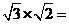 (3)() 2= (4)
(3)() 2= (4)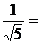 _____
_____
9.函数 中,自变量
中,自变量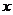 的取值范围是
.
的取值范围是
.
10.若方程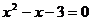 的两根是
的两根是 ,则
,则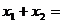 ,
,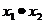 = 。
= 。
11.若关于x的方程x2=m 有解,则m的取值范围是
12.如图,△ABC与△DEF是位似图形,位似比为2∶3,已知AB=4,则DE的长为 ____.

13.若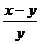 =
= 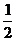 ,则
,则  =
。
=
。
14.关于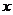 的一元二次方程
的一元二次方程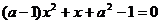 的一个根是0,则
的一个根是0,则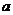 的值为
的值为
15.直角三角形的两直角边长分别为6和8,则重心与斜边中点的距离是 。
16.如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE = 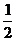 DC。若△DEF的面积为2 ,则□ABCD的面积为 .
DC。若△DEF的面积为2 ,则□ABCD的面积为 .

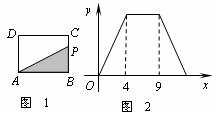
17.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则矩形ABCD的面积是 。
三、解答题(本大题有9小题,共89分)
18.(本题满分18分)
(1)计算:(每小题4分,共8分)
① 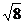 +
+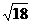 ―
―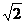 ②
② 
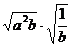
(2)解方程:(每小题5分,共10分)
①x2-6x+1=0. ②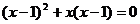
19.(本题满分8分)如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D。此时如果测得BD=60米,DC=30米,EC=25米,求两岸间的大致距离AB.

20.(本题满分8分)已知关于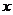 的一元二次方程
的一元二次方程
(1)若-1是方程的一个根,求 的值和方程的另一根;
的值和方程的另一根;
(2)“当 m>0时,方程有两个实数根”的说法正确吗?正确请说明理由。不正确请举出反例。
21.(本题满分8分)已知,D是△ABC的AB边上的一点,BD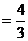 ,AB = 3,BC=2
,AB = 3,BC=2
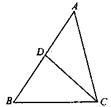
(1)△BCD与△BAC相似吗?说明理由。
(2)若△BCD的面积是4,求△ADC的面积.
22.(本题满8分)学校准备在图书馆后面的场地边建一个矩形车棚,如图ABCD,其中一边利用图书馆的后墙(后墙的长度足够长),并利用已有总长为40米的铁围栏,设BC=x米,矩形车棚的面积为y平方米
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)若按规划要求矩形车棚的面积为300平方米,试分析能否顺利实施?

23.(本题满分8分)抛物线y=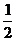 x2+bx-2与x轴交于A、B两点,与y轴交于C点,
x2+bx-2与x轴交于A、B两点,与y轴交于C点,
且A(-1,0)。
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
24.(本题满分9分)设一次函数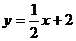 的图象为直线
的图象为直线 ,直线
,直线 与
与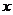 轴、
轴、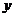 轴分别交于点A、B , 如图:
轴分别交于点A、B , 如图:

(1)求点A和点B的坐标;
(2)直线 过点P(-3,0),若直线
过点P(-3,0),若直线 、
、 与
与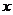 轴围成的三角形和直线
轴围成的三角形和直线 、
、 与
与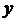 轴围成的三角形相似,求直线
轴围成的三角形相似,求直线 与
与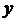 的交点N的坐标。
的交点N的坐标。
25.(本题满分10分)为把产品打入国际市场,某企业决定从下面两个投资方案中选择一个进行投资生产.方案一:生产甲产品,每件产品成本为a万美元(a为常数,且3<a<8),每件产品销售价为10万美元,每年最多可生产200件;方案二:生产乙产品,每件产品成本为8万美元,每件产品销售价为18万美元,每年最多可生产120件。另外,年销售x件乙产品时需上交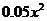 万美元的特别关税。在不考虑其它因素的情况下:
万美元的特别关税。在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润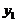 、
、 与相应生产件数x(x为正整数)之间的函数关系式,并指出自变量的取值范围;(4分)
与相应生产件数x(x为正整数)之间的函数关系式,并指出自变量的取值范围;(4分)
(2)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?(6分)
26.(本题满分12分)已知抛物线: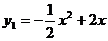 将抛物线
将抛物线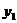 向右平移2个单位,再向上平移1个单位,得到抛物线
向右平移2个单位,再向上平移1个单位,得到抛物线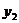 ,
,
(1)求抛物线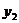 的解析式.
的解析式.
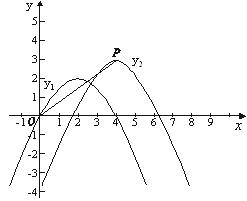
(2)如下图,抛物线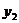 的顶点为P,
的顶点为P,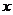 轴上有一动点M,在
轴上有一动点M,在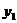 、
、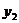 这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由.
这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com