1．下面是一名同学所做的5道练习题：

①（-3）⁰=1；②a³+ a³=a⁶；③（-a⁵）÷（-a ³）= -a²；④4m^-2=1/4m²⑤（xy²）³=x²y⁶．他做对的题数是（    ）

A．0                 B．1                  C．2                  D．3

2．温家宝总理在《政府工作报告》中，讲述了六大民生新亮点，其中之一就是全部免除了西部地区和部分中部地区农村义务教育阶段约52 000 000名学生的学杂费．这个数据保留两个有效数字用科学记数法表示为（    ）

A．52×10⁷                 B．5.2×10⁷           C．5.2×10⁸        D．52×10⁸

3．在-2、-1、0、1、2中任取一个数，恰好使分式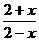有意义的概率是（    ）

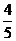A．               B．               C．               D．1

4．已知圆锥的侧面展开图是一个半圆，则这个圆锥的母线长与底面半径之比为（    ）

A．2：1            B．2：1            C．：1        D．：1

5．如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→D→AB连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向是（    ）

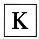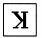A．            B．            C．            D．

请把下列各题的正确答案填写在横线上．

6．函数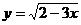中，自变量的取值范围是________．

7．分解因式xy²-2xy+x=________．

8．命题“平行四边形的对角线互相平分”的逆命题是________ ．

9．平面直角坐标系中，已知B（-2，0）关于y轴的对称点为B’，从A（2，4）发出一束光线，经过y轴反射后穿过B’点，此光线在y轴上的入射点的坐标是________．

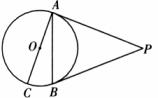
10．如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40⁰，则∠BAC度数是________．

11．计算：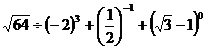

12．求不等式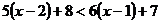的最小整数解．

13．已知关于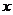的方程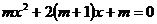有两个实数根，求m的取值范围．

14．在如图所示的直角坐标系中有一个格点△ABC（各顶点都在网格的交点上）．

（1）写出A、B、C分别关于原点O的对称点A’、B’、C’的坐标：

A’的坐标是____________；B’的坐标是____________；C’的坐标是________．

（2）在图中作出△ABC关于原点O的对称图形（要求指出作图结果）．

15．两个全等的含30⁰角和60⁰角的三角尺ADE和三角尺ABC如图所示放置，E、A、C三点在一条直线上，连接BD，取BD的中点M，连接ME、MC．试判断△EMC的形状，并说明理由．

16．《中学生体质健康标准》规定学生体质健康等级标准为：86分以上为优秀，76分～85分为良好，60分～75分为及格，59分以下为不及格．某学校从九年级学生中随机抽取了10％的学生进行了体质健康测试，得分情况如下图：

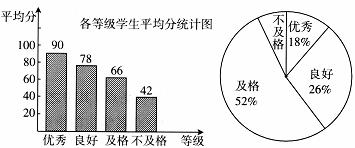
（1）在抽取的学生中不及格人数所占的百分比是_________．

（2）小明按以下方法计算出抽取学生的平均得分是：（90+78+66+42）÷4=69．根据所学的统计知识判断小明的计算是否正确，若不正确，请写出正确的算式（不必计算出结果）．

（3）若不及格学生的总分恰好等于某一个良好等级学生的分数，请估算出该校九年级学生中优秀等级的人数．

17．请你根据图象所提供的信息，解答下面问题：

（1）分别写出,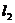中变量随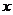变化而变化的情况．

（2）求出一个二元一次方程组，使它满足图象中的条件．

18．福林制衣厂现有24名制作服装的工人，每天都制作某种品牌的衬衫和裤子，每人每天可制作衬衫3件或裤子5条．

（1）若该厂要求每天制作的衬衫和裤子数量相等，则应安排制作衬衫和裤子各多少人?

（2）已知制作一件衬衫可获得利润30元，制作一条裤子可获得利润16元，若该厂要求每天获得利润不少于2100元，则至少需要安排多少名工人制作衬衫?

19．某广告公司要设计一幅周长为12米的矩形广告牌，设计费为每平方米1000元，设矩形的一边长为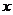米，所花费用为元．

（1）写出与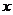之间的函数关系式，并指出自变量的取值范围．

（2）当一边长设计为多少米时，设计费用最大?

五、解答题（本大题共3小题，每小题9分，共27分）

20．如图，在△ABC中，D为AC上一点，CD=2DA，∠BAC=45⁰，∠BDC=60⁰，CE⊥BD，E为垂足，连结AE

（1）写出图中所有相等的线段，并选择其中一对给予证明．

（2）图中有无相似三角形?若有，请写出一对，并加以证明；若没有，请说明理由．

21．上海至成都高速铁路即将动工，工程需要测量汉江某一段的宽度．如图（1），一测量员在江岸边的A处测得对岸岸边的一根标杆B在A的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得∠ACB=68⁰．

（1）求所测之处江的宽度（sin68⁰≈0.93，cos68⁰≈0.37，tan68⁰≈2.48．）．

（2）除（1）的测量方案外，请你再设计一种测量江宽的方案，在图（2）中画出图形，并简要叙述测量工具和测量方法．

22．在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10．点E在下底边BC上，点F在腰AB上．

（1）若EF平分等腰梯形ABCD的周长，设BE长为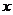，试用含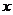的代数式表示△BEF的面积．

（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在，求出此时BE的长；若不存在，请说明理由．

（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分?若存在，求出此时BE的长；若不存在，请说明理由．