
江苏省二??九届初中毕业班第一次调研测试
数 学 试 题
注意事项:
考生在答题前请认真阅读注意事项及各题答题要求
1.本试卷共6页,选择题(第1题~第8题,共8题,计24分),非选择题(第9题~第28题,共20题,计126分)两部分.本次考试时间为120分钟,满分为150分,考试形式为闭卷.
2.答题前,请你务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题纸的指定位置.
3.答案必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其它位置作答一律无效.
一、选择题(本大题共8小题,每小题3分,计24分)
1. 9的算术平方根是……………………………………………………………………( ▲ )
A. ±3 B. 3 C. -3 D. 81
2. 下列计算正确的是……………………………………………………………………( ▲ )
A.  B.
B. 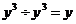 C.
C.  D.
D. 
3. 布袋中的5个红球与10个白球除颜色外完全相同,则从布袋中随机摸出一个球是白球的概率为………………………………………………………………………………………( ▲ )
A. B. C. D. 1
4. 神州7号运行1小时的行程约28600000m,用科学记数法可表示为……………( ▲ )
A. 0.286×108 m B. 2.86×107 m C. 28.6×106 m D. 2.86×105 m
5. 若a<b,则下列不等式中正确的是…………………………………………………( ▲ )
A. a-2>b-2 B. -2 a<-2b C. 2-a>2-b D. m2a>m2b
6. 如果把分式 中的
中的 和
和 都扩大3倍,那么分式的值…………………………( ▲ )
都扩大3倍,那么分式的值…………………………( ▲ )
A. 扩大3倍 B. 缩小3倍 C. 缩小6倍 D. 不变
7. 如图,直线 是一条河,P、Q两地相距8千米,P、Q两地到
是一条河,P、Q两地相距8千米,P、Q两地到 的距离分别为2千米、5千米,欲在
的距离分别为2千米、5千米,欲在 上的某点M处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是…………………………………………( ▲ )
上的某点M处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是…………………………………………( ▲ )


 8. 把图①的纸片折成一个三棱柱,放在桌上如图②所示,则从左侧看到的面为………………………………( ▲ )
8. 把图①的纸片折成一个三棱柱,放在桌上如图②所示,则从左侧看到的面为………………………………( ▲ )
A. Q B. R C. S D. T
二、填空题(本大题共10小题,每小题3分,计30分)
 9. 分解因式:
9. 分解因式: = ▲ .
= ▲ .
10. 如图,在△ABC中,点D、E分别是AB、AC的中点,则△ADE与四边形DBCE的面积比为 ▲ .
11. 函数 中,自变量
中,自变量 的取值范围是 ▲ .
的取值范围是 ▲ .
12. 在你所学过的几何图形中,既是轴对称图形又是中心对称图形的有 ▲ (写出两个).
13. 关于 的一元二次方程
的一元二次方程 有两个相等的实数根,则
有两个相等的实数根,则 的值是 ▲ .
的值是 ▲ .
14. 若等腰三角形中有一个内角等于50°,则这个等腰三角形的顶角的度数为 ▲ .
15. 如图,PA切⊙O于点A,PC过点O且交⊙O于点B、C,若PA=6┩,PB=4┩,则⊙O的半径为 ▲ ┩.



16. 如图,在Rt△ABC中,∠C=90°,AC=3┩,BC=4┩,以BC边所在的直线为轴,将△ABC旋转一周,则所得到的几何体的侧面积是 ▲ ┩2.
17. 如图是2009年6月份的日历,如图那样,用一个圈竖着圈住3个数,如果被圈的三个数的和为39,则这三个数中最大的一个为 ▲ .
18. 已知二次函数 (a为常数)的图象上有三点:A
(a为常数)的图象上有三点:A 、B
、B 、C
、C ,其中
,其中 ,则
,则 的大小关系是 ▲ .
的大小关系是 ▲ .
三、解答题(本大题共10小题,计96分)
19. (本小题满分8分)
20. (本小题满分8分)解方程:
21. (本小题满分8分)请你先化简 ,再从0,-2,2,1中选择一个合适的数代入,求出这个代数式的值.
,再从0,-2,2,1中选择一个合适的数代入,求出这个代数式的值.
22. (本小题满分8分)某校初三年级全体640名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中64名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:
(1)这64名学生培训前考分的中位数所在的等级是 .
(2)估计该校整个初三年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(3)你认为上述估计合理吗?为什么?
答: ,理由: .

23. (本小题满分10分)如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.
(1)请写出三条与BC有关的正确结论(不需要证明);
(2)当∠D=30°,BC=1时,求圆中阴影部分的面积(π≈3.14,≈1.73,结果精确到十分位)

24. (本小题满分10分)商场正在销售 “福娃”玩具和徽章两种奥运商品,已知购买1盒“福娃”玩具和2盒徽章共需145元;购买2盒“福娃”玩具和3盒徽章共需280元.
(1)一盒“福娃”玩具和一盒徽章的价格各是多少元?
(2)某公司准备购买这两种奥运商品共20盒送给幼儿园(要求每种商品都要购买),且购买总金额不能超过450元,请你帮公司设计购买方案.
25. (本小题满分10分)码头工人往一艘轮船上装载货物,装完货物所需的时间y(分钟)与装载速度x(吨/分钟)之间满足反比例函数关系,图象如图所示.
(1)这批货物的质量是多少?
(2)若b-c=40(分钟),请根据图中提供的信息求b、c、d的值.
(3)在(2)的条件下,若轮船到达目的地后,以d(吨/分钟)的速度开始装货,装到一半时,一辆吊车发生故障,因而每分钟少装1吨,那么装满这船货物一共需要多少时间?

26. (本小题满分10分)如图,矩形ABCD的长、宽分别为 和1,且OB=1,点E
和1,且OB=1,点E ,连结AE、ED.
,连结AE、ED.
(1)求经过A、E、D三点的抛物线的表达式;
(2)若以原点为位似中心,将五边形AEDCB放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A′E′D′C′B′;
(3)经过A′、E′、D′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.

27. (本小题满分12分)如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

28. (本小题满分12分)已知:如图1所示,直线 与x轴、y轴相交于C、D两点,直线
与x轴、y轴相交于C、D两点,直线 与x轴、y轴相交于A、B两点,F(4,0)是x 轴上一点,过C点的直线
与x轴、y轴相交于A、B两点,F(4,0)是x 轴上一点,过C点的直线 垂直于x轴,N是直线
垂直于x轴,N是直线 上一点(N点与C点不重合),连结AN.
上一点(N点与C点不重合),连结AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由.
(3)如图2所示,连结NF,求△ AFN外接圆面积的最小值,并求△AFN外接圆面积最小时,圆心G的坐标.





湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com