|
试题详情
8.6个人分乘两辆不同的出租车,如果每辆车最多能乘4个人,则不同的乘车方案有 A.40种
B.50种
C.150种
D.270种 试题详情
9.已知F1、F2的椭圆 的焦点,M为椭圆上一点,MF1垂直于x轴,且 的焦点,M为椭圆上一点,MF1垂直于x轴,且 则该椭圆的离心率为 则该椭圆的离心率为 试题详情
试题详情
试题详情
试题详情
试题详情
12.如图,正三棱锥S―ABC中,侧面SAB与底面ABC所成的二面角等于 ,动点 ,动点 试题详情
P在侧面SAB内,PQ⊥底面ABC,垂足为Q,PQ=PS?sin ,则动点P ,则动点P 的轨迹为 A.双曲线 B.椭圆 C.一段抛物线 D.一段线段 试题详情
 二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.) 二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
试题详情
14.已知过原点的直线与圆 (其中 (其中 为参数)相切,若切点在第二象限,则该直线的方程为 . 为参数)相切,若切点在第二象限,则该直线的方程为 . 试题详情
试题详情
16.已知实数x,y满足约束条件 ,若目标函数 ,若目标函数 只有当 只有当 时取得最大值,则a的取值范围是
. 时取得最大值,则a的取值范围是
. 第Ⅱ卷 试题详情
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
试题详情
 ,且 ,且 . .
试题详情
(Ⅰ)求角 的大小; 的大小; 试题详情
(Ⅱ)若 ,求角 ,求角 的值. 的值. 试题详情
18.(本题12分)在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐. 已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中的 试题详情
概率都是 ,每次命中与否相互独立. ,每次命中与否相互独立. (Ⅰ)求恰好射击5次引爆油罐的概率; 试题详情
(Ⅱ)如果引爆或子弹打光则停止射击,设射击次数为 ,求 ,求 的分布列及 的分布列及 的数学期望. 的数学期望. 试题详情
试题详情
(Ⅰ)求证: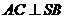 ; ; 试题详情
(Ⅱ)求二面角 的大小. 的大小. 试题详情
20.(本题12分)已知函数 . .
试题详情
(Ⅰ)写出函数 的定义域,并求其单调区间; 的定义域,并求其单调区间;
试题详情
试题详情
试题详情
试题详情
试题详情
的最小正整数 . . 试题详情
试题详情
试题详情
(Ⅰ)求双曲线 的离心率 的离心率 ; ; 试题详情
(Ⅱ)若过焦点 且平行于 且平行于 的直线交双曲线于 的直线交双曲线于 两点,且 两点,且 ,求此时双曲线的方程. ,求此时双曲线的方程. 永昌四中2009届高三年级三摸理科数学答案 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C D C A C A B B A C A C 试题详情
二、填空题:(本大题共4小题,每小题5分,共20分.)
试题详情
三、解答题:(本大题共6小题,共70分.)
试题详情
解: (Ⅰ)由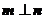 得 得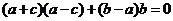 ; .........2分 ; .........2分 试题详情
整理得 .即 .即 . ..........3分 . ..........3分 试题详情
又 . ..........4分 . ..........4分 试题详情
又因为 , , 试题详情
所以 . ..........5分 . ..........5分 试题详情
试题详情
由 . . 试题详情
即 , , 试题详情
所以 . . 试题详情
即 . .............8分 . .............8分 试题详情
因为 ,所以 ,所以 , ........9分 , ........9分 试题详情
故 或 或 . . 试题详情
所以 或 或 . .........10分 . .........10分 试题详情
试题详情
解: (Ⅰ)记“恰好射击5次引爆油罐”的事件为事件 ,则 ,则 试题详情
 .
……………4分 .
……………4分
试题详情
(Ⅱ)射击次数 的可能取值为2,3,4,5.
………………5分 的可能取值为2,3,4,5.
………………5分 试题详情
 ; ;
试题详情
 ; ;
试题详情
 ; ;
试题详情
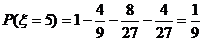 .
………………9分 .
………………9分
试题详情
故 的分布列为 的分布列为 试题详情

2 3 4 5 试题详情
试题详情
试题详情
试题详情
试题详情

…………10分 试题详情
 . .
试题详情
故所求 的数学期望为 的数学期望为 .
…………12分 .
…………12分 试题详情
试题详情
试题详情
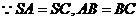 , , 试题详情
试题详情
试题详情
 .
…………………6分 .
…………………6分 试题详情
试题详情
试题详情
试题详情
试题详情
故 为二面角 为二面角 的平面角. ……………………9分 的平面角. ……………………9分 试题详情
试题详情
试题详情
试题详情
在△ 中可得 中可得 , , 试题详情
在△ 中, 中, , , 试题详情
在Rt△ 中, 中, . . 试题详情
 . .
试题详情
试题详情
试题详情
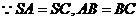 , , 试题详情
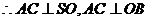 . . 试题详情
试题详情
 平面 平面 . . 试题详情
如图所示建立空间直角坐标系 , , 试题详情
则 . . 试题详情
 . .
试题详情
则 , , 试题详情
 .
………………6分 .
………………6分
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
∵ , , 试题详情
∴ . . 试题详情
令 , , 试题详情
则 .
……………………………………3分 .
……………………………………3分 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情

+ 0 - 试题详情

ㄊ 极大值 ㄋ 试题详情
∴函数 的单调递增区间是 的单调递增区间是 ,单调递减区间是 ,单调递减区间是 . …6分 . …6分 (Ⅱ)由题意可知: 试题详情
 ,
……………………………………7分 ,
……………………………………7分
试题详情
曲线 在点 在点 处的切线的斜率为 处的切线的斜率为 . ……8分 . ……8分 ∴切线方程为: 试题详情
 .
……………………………………9分 .
……………………………………9分
试题详情
∴ .∴ .∴ . ……10分 . ……10分 试题详情
试题详情
试题详情
试题详情
解:(Ⅰ)∵ ( ( ), ), 试题详情
∴ ( ( ).
………………………1分 ).
………………………1分 试题详情
试题详情
∴ . …………………………3分 . …………………………3分 试题详情
∴ .
……………………………………5分 .
……………………………………5分 试题详情
∴ .
……………………………………6分 .
……………………………………6分 (Ⅱ)由(Ⅰ)得 试题详情
 ( ( ). ).
试题详情
∴数列 为首项是 为首项是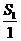 ,公差为1的等差数列. ………………………8分 ,公差为1的等差数列. ………………………8分 试题详情
∴ . . 试题详情
∴ .
……………………………………10分 .
……………………………………10分 试题详情
当 时, 时, . ………………………11分 . ………………………11分 试题详情
当 时,上式也成立. 时,上式也成立.
试题详情
∴ ( ( ). ……………………9分 ). ……………………9分 试题详情
试题详情
故  …10分 …10分 试题详情
要使 都成立 必须且只须 都成立 必须且只须 试题详情
  …………12分 …………12分
试题详情
 22、(本题12分) 22、(本题12分)
试题详情
解: (Ⅰ)由于四边形 是菱形,故 是菱形,故 , , 试题详情
作双曲线的右准线交 于点 于点 , , 试题详情
则 . …………3分 . …………3分 所以离心率 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
即 .
………………7分 .
………………7分 试题详情
试题详情
将直线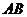 的方程代入到双曲线方程中得 的方程代入到双曲线方程中得 .
…………10分 .
…………10分 试题详情
由 得 得 , , 试题详情
试题详情
|

 则满足
则满足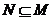 的集合
的集合 的个数是
的个数是  i)=2的复数z对应的点位于
i)=2的复数z对应的点位于 ,则
,则 的值是
的值是 B.
B. C.-
C.- D.
D.
 =(1, x-1),
=(1, x-1), =(x+1,3),则“x=
=(x+1,3),则“x= ∥
∥ ”的
”的 的反函数为
的反函数为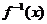 ,则
,则 的值为
的值为 D.-
D.-
 ,
, 为
为 的导函数,那么要得到
的导函数,那么要得到 的图象,只需将
的图象,只需将 的图象
的图象 个单位 B.向右平移
个单位 B.向右平移 个单位 C.向左平移
个单位 C.向左平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位