
江西省南昌市2008―2009学年度高三第二轮复习测试(五)
数 学 试 题
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合 为 ( )
为 ( )
A.{―1,0,1} B.{1} C.{0,1} D.{0}
2.(文)在数列 中,若
中,若 且对任意的
且对任意的 有
有 则数列
则数列 前15项的和为 ( )
前15项的和为 ( )
A. B.30 C.5 D.
B.30 C.5 D.
(理)若复数 是纯虚数,则实数a的值为 ( )
是纯虚数,则实数a的值为 ( )
A. B.13 C.
B.13 C. D.-6
D.-6
3.若 ,则下列不等关系中不能成立的是 ( )
,则下列不等关系中不能成立的是 ( )
A. B.
B. C.
C. D.
D.
4.设a,b,c分别是△ABC三个内角A,B,C所对的边,若a=1, ,则∠A=30°是∠B=60°的 ( )
,则∠A=30°是∠B=60°的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.当a,b,c是空间三条直线, 是空间两个平面,则下列命题中,逆命题不成立的是
是空间两个平面,则下列命题中,逆命题不成立的是
( )
A.当
B.当
C.当
D.当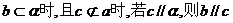
6.设 的展开式的各项系数之和为M。而二项式系数之和为N,且
的展开式的各项系数之和为M。而二项式系数之和为N,且 ,则展开式中含x2项的系数为 ( )
,则展开式中含x2项的系数为 ( )
A.150 B.-150 C.250 D.-250
7. 将A、B、C、D四个球放入编号为1,2,3的三个盒子中,每个盒子中至少放一个球且A、B两个球不能放在同一盒子中,则不同的放法有 ( )
A.15 B.18 C.30 D.36
8.(文)已知 的夹角为60°,则直线
的夹角为60°,则直线
 的位置关系是 ( )
的位置关系是 ( )
A.相交 B.相切 C.相离 D.不能确定
(理)统计表明,某省某年的高考数学成绩 ,现随机抽查100名考生的数学试卷,则成绩超过120分的人数的期望是 ( )
,现随机抽查100名考生的数学试卷,则成绩超过120分的人数的期望是 ( )
(已知 )
)
A.9或10人 B.6或7人 C.3或4人 D.1或2人
9.设A={1,2,…,10},若“方程 ,且方程至少有一根
,且方程至少有一根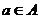 ”,就称该方程为“漂亮方程”,则“漂亮方程”的个数为 ( )
”,就称该方程为“漂亮方程”,则“漂亮方程”的个数为 ( )
A.8 B.10 C.12 D.14
10.已知 的离心率为
的离心率为
( )
A. B.
B. C.
C. D.
D.
11.以正方体的任意三个顶点为顶点作三角形,从中椭机地取出两个三角形,则这两个三角形不共面的概率为 ( )
A. B.
B. C.
C. D.
D.
12.关于函数 有下列命题:
有下列命题:
①
② 是以
是以 为最小正周期的周期函数;
为最小正周期的周期函数;
③ 在区间
在区间 上是减函数;
上是减函数;
④将函数 个单位后,与已知函数的图象重合。
个单位后,与已知函数的图象重合。
其中正确命题的序号是 ( )
A.①②③ B.①② C.②③④ D.①②③④
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中横线上)
|